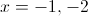We know that \(\displaystyle -\frac{a}{b}\) is equivalent to \(\displaystyle \frac{-a}{b}\) or \(\displaystyle \frac{a}{-b}\).

By this property, there is no way to get \(\displaystyle \frac{x+5}{2x+3}\) from \(\displaystyle -\frac{x-5}{2x+3}\).

Therefore the correct answer is \(\displaystyle \frac{x+5}{2x+3}\).

Because the denominator cannot be zero, the domain is all other numbers except for 1, or

\(\displaystyle x\neq1\)

This problem is a lot simpler if we factor all the expressions involved before proceeding:

\(\displaystyle \frac{x^2-1}{x^2+4x+2}\div\frac{x^2+2x+1}{x^2+3x+2} \vspace{5mm}\\ = \frac{(x+1)(x-1)}{(x+2)(x+2)}\div\frac{(x+1)(x+1)}{(x+2)(x+1)}\)

Next let's remember how we divide one fraction by another—by multiplying by the reciprocal:

\(\displaystyle \frac{(x+1)(x-1)}{(x+2)(x+2)}\div\frac{(x+1)(x+1)}{(x+2)(x+1)} \vspace{5mm}\\ = \frac{(x+1)(x-1)}{(x+2)(x+2)}\times\frac{(x+2)(x+1)}{(x+1)(x+1)}\) 

In this form, we can see that a lot of terms are going to start canceling with each other. All that we're left with is just \(\displaystyle \frac{x-1}{x+2}\).

The rational expression is a ratio of two polynomials.  

\(\displaystyle \frac{A(x)}{B(x)}\)

The denominator cannot be zero.

An example of a rational expression is:

\(\displaystyle \frac{x^2+x-5}{x+8}\)

The answer is:  

\(\displaystyle \textup{The ratio of two polynomials that cannot have a zero denominator.}\)

If \(\displaystyle \left ( x-1 \right ) = 0\) or \(\displaystyle \left ( x+2 \right ) =0\), the denominator is 0, which makes the expression undefined.

 This happens when x = 1 or when x = -2.

Therefore the correct answer is \(\displaystyle x = 1, -2\).

In order to simplify the expression \(\displaystyle \frac{4}{x+6}+ \frac{9}{x+4}\), we need to ensure that both terms have the same denominator. In order to do so, find the Least Common Denominator (LCD) for both terms and simplify the expression accordingly:

\(\displaystyle \frac{4(x+4)}{(x+6)(x+4)} + \frac{9(x+6)}{(x+4)(x+6)}\)

\(\displaystyle =\frac{4(x+4) +9(x+6)}{(x+6)(x+4)}\)

\(\displaystyle =\frac{4x+16+9x+54}{x^{2}+10x+24}\)

\(\displaystyle =\frac{13x+70}{x^{2}+10x+24}\)

In order to simplify the expression  \(\displaystyle \frac{x-7}{x+3}+ \frac{9}{x^{2}+10x+21}\), first note that the denominators in both terms share a factor:

\(\displaystyle \frac{x-7}{x+3}+ \frac{9}{(x+3)(x+7)}\)

Find the Least Common Denominator (LCD) of both terms:

\(\displaystyle \frac{(x-7)(x+7)}{(x+3)(x+7)}+ \frac{9}{(x+3)(x+7)}\)

\(\displaystyle =\frac{x^{2}-49}{x^{2}+10x+21}+ \frac{9}{x^{2}+10x+21}\)

Finally, combine like terms:

\(\displaystyle \frac{x^{2}-49+9}{x^{2}+10x+21}\)

\(\displaystyle =\frac{x^{2}-40}{x^{2}+10x+21}\)

\(\displaystyle \frac{5}{x+2} -\frac{10}{x+3}\)

1. Create a common denominator between the two fractions.

\(\displaystyle \frac{5(x+3)}{(x+2)(x+3)} -\frac{10(x+2)}{(x+3)(x+2)}\)

2. Simplify.

\(\displaystyle =\frac{5(x+3)-10(x+2)}{(x+2)(x+3)}\)

\(\displaystyle =\frac{5x+15-10x-20}{x^{2}+5x+6}\)

\(\displaystyle =\frac{-5x-5}{x^{2}+5x+6}\)

For a rational expression to be undefined, the denominator must be equal to \(\displaystyle 0\).

1. Set the denominator equal to \(\displaystyle 0\).

\(\displaystyle (x+2)(x-10)=0\)

2. Set the factors equal to \(\displaystyle 0\) and solve for \(\displaystyle x\).

\(\displaystyle x+2=0\)

\(\displaystyle x=-2\)

and

\(\displaystyle x-10=0\)

\(\displaystyle x=10\)

A rational expression is undefined when the denominator is zero.

\(\displaystyle x-1=0\)

\(\displaystyle x=1\)

The denominator is zero when \(\displaystyle x=1\).