All Algebra II Resources
Example Questions
Example Question #601 : Functions And Graphs
Try without a calculator.
The graph of a function with the given equation forms a parabola that is characterized by which of the following?
None of these
Concave upward
Concave downward
Concave to the right
Concave to the left
Concave to the left
The graph of an equation of the form
is a horizontal parabola. Whether it is concave to the left or to the right depends on the sign of 

Example Question #55 : Polynomial Functions
How many 
One
Five
Ten
Two
Zero
One
The graph of a quadratic function 



The number of 


The discriminant is equal to zero, so the quadratic equation has one real zero, and the graph of 

Example Question #56 : Polynomial Functions
The vertex of the graph of the function
appears in __________.
Quadrant III
Quadrant II
None of these
Quadrant I
Quadrant IV
Quadrant I
The graph of the quadratic function 

Set 


Evaluate 
The vertex has a positive 

Example Question #57 : Polynomial Functions
The vertex of the graph of the function
appears in __________.
Quadrant II
Quadrant I
None of these
Quadrant III
Quadrant IV
Quadrant III
The graph of the quadratic function 

Set 


Evaluate 
The vertex has a negative 

Example Question #602 : Functions And Graphs
What transformations have been enacted upon 

vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 2
horizontal translation 6 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 2
horizontal translation 3 units right
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
Example Question #2 : Transformations Of Polynomial Functions
Define 

Find 
By definition, 
Example Question #603 : Functions And Graphs
Define 

Find 
By definition, 
Example Question #4 : Transformations Of Polynomial Functions
Write the transformation of the given function moved five units to the left:
To transform the function horizontally, we must make an addition or subtraction to the input, x. Because we are asked to move the function to the left, we must add the number of units we are moving. This is the opposite of what one would expect, but if we are inputting values that are to the left of the original, they are less than what would have originally been. So, to counterbalance this, we add the units of the transformation.
For our function being transformed five units to the left, we get
Example Question #604 : Functions And Graphs
Write the transformation of the given function flipped, and moved one unit to the left:
To transform a function horizontally, we must add or subtract the units we transform to x directly. To move left, we add units to x, which is opposite what one thinks should happen, but keep in mind that to move left is to be more negative. To flip a function, the entire function changes in sign.
After making both of these changes, we get
Example Question #6 : Transformations Of Polynomial Functions
Transform the function by moving it two units up, and five units to the left:
To transform a function we use the following formula,
where h represents the horizontal shift and v represents the vertical shift.
In this particular case we want to shift to the left five units,
and vertically up two units,

Therefore, the transformed function becomes,

Certified Tutor
All Algebra II Resources

















![g(x)=4[2(x-3)]^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/155687/gif.latex)













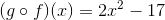












![-[(x-1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702385/gif.latex)
![-[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702384/gif.latex)
![[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702386/gif.latex)
![[(x-1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702387/gif.latex)
![-[(x+1)^2+4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/702536/gif.latex)










