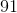When solving functions within functions, we begin with the innermost function and work our way outwards. Therefore:

and

This problem relies on our knowledge of a radical expression  equal to . The functions are subbed into one another in order from most inner to most outer function.

and

In problems with functions within one another, we must first solve the innermost function and then proceed outwards. Therefore, the first step is solving  :

Now, we must find the values of :

Because our x term is squared in this function, both values end up being the same. Therefore, 59 is our final answer.

Beginning with the innermost function, we must first solve for :

We then take this value and plug it into :

This has no value in the real number plane, and the answer is therefore undefined.

Substituting -x into f(x).  This has no effect on the 1st and 3rd terms.  This changes the sign of the middle term.

A polynomial in standard form is written in descending order of the power. The highest power should be first, and the lowest power should be last.

The answer has the powers decreasing from four, to two, to one, to zero.

Expression 5 has the term , which violates the definition of a polynomial.  The exponent must be a whole number.

When finding the x-intercepts for a function, this is where the function crosses the x-axis, which means that  or  must equal zero. 

So we first set  which gives us: 

Now in order to solve this equation, we must break down the polynomial using the "Factor by Grouping" Method. 

To "Factor by Grouping" you must put the polynomial in standard form and then group into to pairs of binomials. 

After doing this, one can see that there is a common factor in each group. 

When an  is taken out of the first pair we are left with  and, 

when a  is taken out of the second pair we are left with  again. 

The goal is to make each the same and we now have two . 

This is now a common factor on this side of the equation, so we can take out the common factor  and we get ths result. 

We can now find the x-intercepts by remembering that we origianilly set this all equal to 0. 

In order for this product to equal zero, either the first or second parentheses needs to equal zero, so we set each equal to zero and solve. 

 and .

After taking the square root of both sides for  you get .

Substitute 5y in for every x:

.

Simplify:

Square the first term: 

Distribute the coefficients: 

Substitute  for  in the original equation:

.

Use FOIL or the Square of a Binomial Rule to find .

Recall that FOIL stands for the multiplication between the First components in both binomials followed by the Outer components, then the Inner components, and lastly the Last components.

Then, Distribute: .

Combine like terms to simplify: