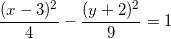To determine which direction a hyperbola opens, first get the equation into standard form for a conic section:

This equation gives us a hyperbola when the coefficient in front of either the x-squared or the y-squared term (but not both!) is negative. In this problem, the coefficient in front of the x-squared term is positive, but the coefficient of the y-squared term is negative. Here are the rules for hyperbola directions:

• If the coefficient of the x-squared term is positive but the coefficient of the y-squared term is negative, this is a hyperbola that opens horizontally.
• If the coefficient of the x-squared term is negative but the coefficient of the y-squared term is positive, this is a hyperbola that opens vertically.

Thus, we have a graph of a horizontal hyperbola.

The first thing we need to find for this hyperbola is the center. This is simply the point where and  both equal , which is . Since the  term is the positive one, the hyperbola opens horizontally, which means we need to look at the denominator of that  term. 

The denominator is which is , so our vertices are , or 

 and .

The standard form of a hyperbola is 

or the similar form with a positive  term and negative  term. So to start out getting this equation in standard form, we must complete the square on the quadratics in  and .

the coefficient of is , so completing the square we get 

and similarly with we get 

and so our starting expression can be written as 

Dividing by  on both sides we get the standard representation of the hyperbola, 

We start by noticing that our hyperbola is given in the following form:

In order to determine the vertices of the hyperbola, we must first locate its center. Using the standard form given above, we know the center of the hyperbola occurs at the point (h,k), so for the equation given in the problem the center is at (2,-3). Now that we know the location of the hyperbola's center, our next step is to determine how far the vertices are from the center of the hyperbola. Looking at our equation, we can see it is in the form where the x term occurs first, which means the hyperbola opens left and right as opposed to up and down (which would be the case if the y term occurred first. Given this information, we know the vertices of the hyperbola are going to be a distance  to the left and right of the center. The denominator of the x term in the hyperbolic equation is 16, which means  is equal to 4, so the vertices of the hyperbola will be 4 units to the left and right of the center (2,-3), which gives us:

and

Rewrite in standard form and factor:

The zeroes of the polynomial are therefore , so we test one value in each of three intervals , , and  to determine which ones are included in the solution set.

:

Test :

False;  is not in the solution set.

:

Test 

True;  is in the solution set

:

Test :

False;  is not in the solution set.

Since the inequality symbol is , the boundary points are not included. The solution set is the interval .

The first step of questions like this is to get the quadratic in its standard form. So we move the  over to the left side of the inequality:

This quadratic can easily be factored as. So now we can write this in the form

and look at each of the factors individually. Recall that a negative number times a negative is a positive number. Therefore the boundaries of our solution interval is going to be when both of these factors are negative.  is negative whenever , and is negative whenever . Since , one of our boundaries will be . Remember that this will be an open interval since it is less than, not less than or equal to.

Our other boundary will be the other point when the product of the factors becomes positive. Remember that is positive when , so our other boundary is . So the solution interval we arrive at is 

When asked to solve for x we need to isolate x on one side of the equation.

To do this our first step is to subtract 7 from both sides.

From here, we divide by 4 to solve for x.

When asked to solve for y we need to isolate the variable on one side and the constants on the other side.

To do this we first add 9 to both sides.

From here, we divide by -12 to solve for y.

The region  contains only  values which are greater than or equal to those on the line , so its  values are .

Also, the region contains only  values which are less than or equal to those on the line , so its  values are .

The region  contains only  values which are greater than or equal to those on the line , so its  values are .

Similarly, the region contains only  values which are less than or equal to those on the line , so its  values are .