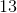TACHS Math : TACHS: Math and Ability
Study concepts, example questions & explanations for TACHS Math
All TACHS Math Resources
Example Questions
Example Question #3 : Geometry
A square has perimeter 24 feet. Give its area.
144 square feet
36 square feet
576 square feet
18 square feet
36 square feet
The perimeter of a figure is the sum of the lengths of its sides. A square comprises four sides of equal length, so, if the perimeter of the square is 24 feet, then each side has length
The area of the square is equal to the length of a side multiplied by itself, so the area of this square is
Example Question #2 : Geometry
Jennifer wants to wallpaper her room which is made up for four rectangular walls each measuring at 
Start by finding out the total square footage of wallpaper needed.
Find the area of one wall. Recall that in order to find the area of a rectangle, you must multiply the length by the width.
Since we have four identical walls,
Now divide this by the amount of square feet covered by each roll of wallpaper to find how many rolls are needed.
Example Question #4 : Geometry
Find the area of a circle with the following radius:
The area of a circle can be calculated using the following formula:
In this formula the radius is denoted by the variable, 
Substitute in the known variables and solve for the circle's area.
Example Question #33 : Tachs: Math And Ability
Which is equal to the radius of a circle with area
The formula for the area 
To find the radius 
Now, find the square root of both sides. Since 
The radius of the given circle is 20.
Example Question #5 : Geometry
To determine whether a machine on an assembly line is filling bottles with the correct amount of soda, twenty bottles are selected. The tenth bottle and every tenth bottle after that are taken off the line and examined.
This is an example of which kind of sampling?
Cluster sampling
Stratified sampling
Convenience sampling
Systematic sampling
Systematic sampling
The sample in this scenario is selected from the population by choosing obects that occur at regular intervals. That makes this an example of systematic sampling.
Example Question #6 : Geometry
What is the area of a circle that has a diameter of 
Recall how to find the area of a circle:
To find the length of the radius, divide the diameter by two.
Now, plug it into the equation for the area of a circle.
Example Question #7 : Geometry
Calculate the volume of a sphere with the following radius:
We can calculate the the volume of a sphere using the following formula:
in this formula the variable, 
Substitute in the known radius and calculate the volume.
Simplify.
Solve.
Example Question #31 : Math
Give the median of the following six scores:
83, 87, 99, 90, 82, 84
To find the median of a group of scores, first, arrange the scores from least to greatest:
There are an even number of scores, so the median is the mean of the two scores that fall in the middle, which are noted in red above. Add the scores and divide by two:
Example Question #2 : Statistics
Over the course of a grading period, Kim had a total of 
Recall how to find the average of a set of numbers:
Thus, we can write the following to solve for the average of Kim's test scores:
Kim has a 
Example Question #32 : Math
What is the probability of rolling a one on a fair die?
Cannot be determined
In order to solve this problem, we need to discuss probabilities. A probability is generally defined as the chances or likelihood of an event occurring. It is calculated by identifying two components: the event and the sample space. The event is defined as the favorable outcome or success that we wish to observe. On the other hand, the sample space is defined as the set of all possible outcomes for the event. Mathematically we calculate probabilities by dividing the event by the sample space:
Let's use a simple example: the rolling of a die. We want to know the probability of rolling a one. We know that the sample space is six because there are six sides or outcomes to the die. Also, we know that there is only a single side with a value of one; therefore,
Now, let's convert this into a percentage:
All TACHS Math Resources
