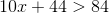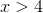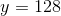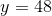Make sure to follow the order of operations. 

Start by simplifying what is found in the parentheses.

Next, simplify any exponents.

Next, simplify any multiplication and division.

Finally, simplify any addition and subtraction.

Make sure you follow the order of operations (PEMDAS: parentheses, exponents, multiplication, division, addition, and subtraction—from the left to the right).

Start by simplifying what's found within the parentheses:

Next, simplify any multiplication and division.

Finally, simplify any addition and subtraction.

Recall what a probability is:

Start by finding the probability of rolling either  or  on a die. Since there are a total of  different outcomes, and we only want these two, the probability must be .

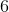
Next, find the probability of getting heads on a coin flip. Since we only want heads and there are only  possible outcomes on a coin flip, the probability of getting heads is .

Since the question wants the probability of both events occurring, you must multiply the probabilities together.

In algebra an inequality is a relationship that holds through different values of a variable. An inequality is considered to be solved when the variable is isolated to one side of the inequality. We will do this by performing the reverse of the operations that were done to the variable. It is important to note that what is done to one side of the inequality needs to be done on the other. 

Let's start by writing the inequality. 

Subtract  from both sides of the inequality. 

Divide each side of the inequality by .

Solve.

The variable is greater than four.

In order to solve this problem we need isolate the variable on the left side o the equation. We will do this by performing the reverse of the operations that were done to the variable. It is important to note that what is done to one side of the equation needs to be done on the other. 

Let's start by writing the equation. 

Subtract  from both sides of the equation.

Multiply both sides of the equation by .

Solve.

Start by subtracting  from both sides.

Next, add  to both sides of the equation.

Finally, divide both sides by .

Start by subtracting both sides by .

Next, subtract both sides by .

Finally, divide both sides by .

Isolate the on the left side of the equation by performing the same steps on both sides. These steps should be the opposite of the operations performed on .

Multiplication precedes addition in the order of operations, so reverse the addition of 16 by subtracting 16 from both sides:

Now reverse multiplication by 2 by dividing by 2:

Perimeters can be calculated by adding together the side lengths of a polygon. A square has four sides that are all the same length, therefore, we can write the following formula to solve for the perimeter.

We can rewrite this equation as the following:

In these equations the variable, , represents side length.

Substitute the known side length and solve.

In order to find the circumference of a circle we will use the following formula:

In this equation, the variable, , represent's the circle's radius.

Substitute in for the circle's radius.

Simplify and solve.