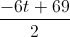We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : How To Find The Area Of A Pentagon

Find the area of a regular pentagon with a side length of and an apothem of .

Possible Answers:

180

120

240

Correct answer:

120

Explanation:

To find the area of a regular polygon,

$\text{Area}=\frac{1}{2}(Perimeter)(apothem)$

To find the perimeter of the pentagon,

$\text{Perimeter}=5(side)$

For the given pentagon,

$\text{Perimeter}=5\times 12=60$

So then, to find the area of the pentagon,

$\text{Area}=\frac{1}{2}(60)(4)=120$

Report an Error

Example Question #1 : How To Find The Perimeter Of A Pentagon

A pentagon with perimeter 54 has three congruent sides of length 2t-5 ; its other two sides are congruent to each other. Give the length of each of those other two sides in terms of .

Possible Answers:

$\frac{- 6t+ 39 }{2}$

$\frac{- 6t+ 59 }{2}$

- 6t+ 69

- 6t+ 39

$\frac{- 6t+ 69 }{2}$

Correct answer:

$\frac{- 6t+ 69 }{2}$

Explanation:

The perimeter of a polygon is the sum of the lengths of its sides. If we let be the length of one of those other two sides, we can set up this equation and solve for :

2X + 3 (2t-5) = 54

$2X + 3 \cdot 2t-3 \cdot 5 = 54$

2X +6t-15 = 54

2X +6t-15 + 15 - 6t= 54+ 15 - 6t

2X =69- 6t

$2X \div 2 =\left ( 69- 6t \right )\div 2$

$X =\frac{- 6t+ 69 }{2}$

Report an Error

Example Question #991 : Ssat Upper Level Quantitative (Math)

A regular pentagon has perimeter 7 meters. Give the length of one side in millimeters.

Possible Answers:

$1,400 \textrm{ mm}$

$1,200 \textrm{ mm}$

$2,100 \textrm{ mm}$

$1,800 \textrm{ mm}$

$1,500 \textrm{ mm}$

Correct answer:

$1,400 \textrm{ mm}$

Explanation:

One meter is equal to 1,000 millimeters, so the perimeter of 7 meters can be expressed as:

7 meters = $7 \times 1,000 = 7,000$ millimeters.

Since the five sides of a regular pentagon are congruent, divide by 5:

$7,000 \div 5 = 1,400$ millimeters.

Report an Error

Example Question #1 : How To Find The Perimeter Of A Pentagon

A regular pentagon has perimeter 42 meters. What is the length of one side in centimeters?

Possible Answers:

840

8400

2100

210

Correct answer:

840

Explanation:

One meter is equal to 100 centimeters, so the perimeter of 42 meters can be expressed as follows:

meters $=42\times 100=4200$ centimeters

In a regular pentagon, all sides are equal in length. Divide the perimeter by 5 to get the length of each side:

$4200\div 5=840$ centimeters

Report an Error

Example Question #2 : How To Find The Perimeter Of A Pentagon

The perimeter of a pentagon is 4t-4 . The pentagon has three congruent sides of length meters. Its other two sides are congruent to each other, each with a length of .

Find .

Possible Answers:

Correct answer:

Explanation:

The perimeter of a polygon is sum of the lengths of its sides. In this pentagon, three sides have the same length of 4 and two others have the same length of . So we can write:

$Perimeter=4t-4=3\times 4+2\times t$

Now we should solve this equation for :

4t-4=12+2t

4t-2t=12+4

2t=16

t=8

Report an Error

Example Question #3 : How To Find The Perimeter Of A Pentagon

A pentagon with perimeter 40 meters has two congruent sides of length 3t+5 . Its other three sides are congruent to each other. Give the length of each of the other three sides in terms of .

Possible Answers:

2t-10

t-5

5-2t

10-2t

5-t

Correct answer:

10-2t

Explanation:

The perimeter of a polygon is the sum of the lengths of its sides. Let:

length of one of those other three sides

Now we have:

$Perimeter=40=2\times (3t+5)+3\times x$

40=6t+10+3x

40-10-6t=3x

30-6t=3x

10-2t=x

So the length of each of those other three sides is 10-2t

Report an Error

Example Question #4 : How To Find The Perimeter Of A Pentagon

Two sides of a pentagon have a length of t-1 , and three other sides have the length of t+1 . Give the perimeter of the pentagon in terms of .

Possible Answers:

5t+1

5t+2

5t-1

10t+1

10t-1

Correct answer:

5t+1

Explanation:

The perimeter of a polygon is the sum of the lengths of its sides. So we can write:

$Perimeter=2\times (t-1)+ 3\times (t+1)$

=2t-2+3t+3

=5t+1

Report an Error

Example Question #5 : How To Find The Perimeter Of A Pentagon

Each exterior angle of a pentagon is 72 degrees and the length of one side is 4 meters. Give the perimeter of the pentagon.

Possible Answers:

Correct answer:

Explanation:

As each exterior angle of the pentagon is 72 degrees, each interior angle would be

$180-72=108^{\circ}$

That means all of the interior angles of the pentagon are identical, so we have a regular pentagon.

The perimeter of a polygon is the sum of the lengths of its sides. So the perimeter of a regular pentagon is ; where is the length of a side.

So we get:

$Perimeter=5a=5\times 4=20$ meters

Report an Error

Example Question #11 : Perimeter Of Polygons

A pentagon has four congruent sides of length $\frac{t^2}{4}-1$ . The length of the fifth side is meters.

Give the perimeter of the pentagon.

Possible Answers:

t^2

t^2+4

4t^2

4t^2-4

Correct answer:

t^2

Explanation:

The perimeter of a polygon is the sum of the lengths of its sides. So we can write:

$Perimeter=4\left ( \frac{t^2}{4}-1 \right )+4$

$=4\times \frac{t^2}{4}-4\times 1+4$

=t^2-4+4

=t^2

Report an Error

Example Question #771 : Geometry

The sidelength of a square is equal to 2t - 17 . Give its perimeter in terms of .

Possible Answers:

6t - 51

4t - 34

2t - 68

8t - 68

8t - 17

Correct answer:

8t - 68

Explanation:

The perimeter of a square is four times its sidelength, so the perimeter of this square is

$4\left ( 2t - 17 \right ) = 4 \cdot 2t - 4 \cdot17 = 8t - 68$ .

Report an Error

View SSAT- Upper Level Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View SSAT- Upper Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View SSAT- Upper Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in New York City, LSAT Tutors in Houston, English Tutors in Boston, Chemistry Tutors in Dallas Fort Worth, MCAT Tutors in New York City, GRE Tutors in New York City, SAT Tutors in Miami, Math Tutors in Seattle, English Tutors in Seattle, English Tutors in San Francisco-Bay Area

Popular Courses & Classes

GRE Courses & Classes in Los Angeles, ACT Courses & Classes in New York City, ISEE Courses & Classes in Miami, SAT Courses & Classes in Denver, GMAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, MCAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Seattle

Popular Test Prep

ACT Test Prep in New York City, LSAT Test Prep in Denver, LSAT Test Prep in Houston, GRE Test Prep in San Diego, MCAT Test Prep in Houston, SSAT Test Prep in Seattle, MCAT Test Prep in Los Angeles, ISEE Test Prep in Boston, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #11 : How To Find The Area Of A Pentagon

Example Question #1 : How To Find The Perimeter Of A Pentagon

Example Question #991 : Ssat Upper Level Quantitative (Math)

Example Question #1 : How To Find The Perimeter Of A Pentagon

Example Question #2 : How To Find The Perimeter Of A Pentagon

Example Question #3 : How To Find The Perimeter Of A Pentagon

Example Question #4 : How To Find The Perimeter Of A Pentagon

Example Question #5 : How To Find The Perimeter Of A Pentagon

Example Question #11 : Perimeter Of Polygons

Example Question #771 : Geometry

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: