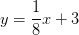SSAT Upper Level Math : Geometry
Study concepts, example questions & explanations for SSAT Upper Level Math
All SSAT Upper Level Math Resources
Example Questions
Example Question #3 : How To Find The Slope Of Parallel Lines
What is the slope of a line that is parallel to the line 11x + 4y - 2 = 9 – 4x ?
We rearrange the line to express it in slope intercept form.
Any line parallel to this original line will have the same slope.
Example Question #21 : Parallel Lines
In the standard (x, y) coordinate plane, what is the slope of a line parallel to the line with equation 
Parallel lines will have equal slopes. To solve, we simply need to rearrange the given equation into slope-intercept form to find its slope.
The slope of the given line is 
Example Question #204 : Geometry
What is the slope of a line that is parallel to the line 
Parallel lines have the same slope. The question requires you to find the slope of the given function. The best way to do this is to put the equation in slope-intercept form (y = mx + b) by solving for y.
First subtract 6x on both sides to get 3y = –6x + 12.
Then divide each term by 3 to get y = –2x + 4.
In the form y = mx + b, m represents the slope. So the coefficient of the x term is the slope, and –2 is the correct answer.
Example Question #156 : Lines
Line 
Any line that is parallel to a line 
Example Question #5 : How To Find The Slope Of Parallel Lines
Which of the following is a line that is parallel to the line 
For a given line 
Example Question #6 : How To Find The Slope Of Parallel Lines
What is the slope of the line 
In order to most easily determine the slope, let's turn this equation into its slope-intercept form 
We can start by subtracting 
Then, we can divide the entire equation by 
Therefore, 
Example Question #31 : Parallel Lines
Which of the following equations gives a line that is parallel to the line with the equation 
Two lines are parallel when they have the same slope. Because the slope of the given line is 
Example Question #211 : Geometry
A line has the equation 
The slope of the second line must be 
To find the equation of this second line, just plug in the given point into the standard form 
Now we have all the parts needed to write the equation for the second line:
Example Question #3 : How To Find The Equation Of A Parallel Line
Line 
Since lines 
Thus, the equation of line 
Example Question #2 : Coordinate Geometry
There is a line defined by the equation below:
There is a second line that passes through the point 
Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.
3x + 4y = 12
4y = –3x + 12
y = –(3/4)x + 3
slope = –3/4
We know that the second line will also have a slope of –3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.
y = mx + b
2 = –3/4(1) + b
2 = –3/4 + b
b = 2 + 3/4 = 2.75
Plug the y-intercept back into the equation to get our final answer.
y = –(3/4)x + 2.75
Certified Tutor
All SSAT Upper Level Math Resources
