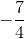Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #174 : Coordinate Geometry

Find the equation of the line that passes through the point (-2, 5) and is parallel to the line with the equation y=-x-2 .

Possible Answers:

y=x+3

y=x-4

y=-x+3

y=-x+6

Correct answer:

y=-x+3

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

Next, plug in the point given by the question to find the y-intercept of the line.

5=-1(-2)+b

b+2=5

b=3

Now, we can write the equation for the line: y=-x+3

Report an Error

Example Question #175 : Coordinate Geometry

Find the equation of the line that passes through the point (-2, 3) and is parallel to the line with the equation $y=\frac{1}{2}x-2$ .

Possible Answers:

y=2x-1

y=-2x+4

$y=\frac{1}{2}x-2$

$y=\frac{1}{2}x+4$

Correct answer:

$y=\frac{1}{2}x+4$

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be $\frac{1}{2}$ .

Next, plug in the point given by the question to find the y-intercept of the line.

$3=\frac{1}{2}(-2)+b$

b-1=3

b=4

Now, we knwo the equation of the line must be $y=\frac{1}{2}x+4$ .

Report an Error

Example Question #176 : Coordinate Geometry

Find the equation of the line that passes through the point (2, 8) and is parallel to the line with the equation y=4x-1 .

Possible Answers:

$y=-\frac{1}{4}x$

y=4x

y=4x-2

$y=\frac{1}{4}x+2$

Correct answer:

y=4x

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

Next, plug in the point given by the question to find the y-intercept of the line.

8=4(2)+b

b+8=8

b=0

Thus, the equation of the line must be y=8x .

Report an Error

Example Question #177 : Coordinate Geometry

Find the equation of the line that passes through the point (10, 2) and is parallel to the line with the equation $y=\frac{1}{5}x-2$ .

Possible Answers:

$y=\frac{1}{5}x$

y=5x-1

y=-5x+2

$y=\frac{1}{5}x-6$

Correct answer:

$y=\frac{1}{5}x$

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be $\frac{1}{5}$ .

Next, plug in the point given by the question to find the y-intercept of the line.

$2=\frac{1}{5}(10)+b$

b+2=2

b=0

The equation of the line is $y=\frac{1}{5}x$ .

Report an Error

Example Question #11 : How To Find The Equation Of A Parallel Line

Find the equation of the line that passes through the point (3, 1) and is parallel to the line with the equation $y=\frac{1}{3}x-9$ .

Possible Answers:

$y=\frac{1}{3}x+2$

$y=-\frac{1}{3}x$

$y=\frac{1}{3}x$

y=-3x

Correct answer:

$y=\frac{1}{3}x$

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be $\frac{1}{3}$ .

Next, plug in the point given by the question to find the y-intercept of the line.

$1=\frac{1}{3}(3)+b$

b+1=1

b=0

The equation of the line is $y=\frac{1}{3}x$ .

Report an Error

Example Question #451 : Ssat Upper Level Quantitative (Math)

Find the equation of the line that passes through the point $\left(\frac{1}{2}, 4\right)$ and is parallel to the line with the equation y=2x-1 .

Possible Answers:

y=2x-2

$y=\frac{1}{2}x+2$

$y=-\frac{1}{2}x-2$

y=2x+3

Correct answer:

y=2x+3

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

Next, plug in the point given by the question to find the y-intercept of the line.

$4=\frac{1}{2}(2)+b$

b+1=4

b=3

Now, we know the equation of the line must be y=2x+3 .

Report an Error

Example Question #181 : Coordinate Geometry

Find the equation of the line that passes through the point $\left(2, \frac{1}{4}\right)$ and is parallel to the line with the equation $y=\frac{1}{8}x-2$ .

Possible Answers:

$y=\frac{1}{8}x-8$

y=-8x

$y=\frac{1}{8}x$

$y=\frac{1}{8}x+3$

Correct answer:

$y=\frac{1}{8}x$

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be $\frac{1}{8}$ .

Next, plug in the point given by the question to find the y-intercept of the line.

$\frac{1}{4}=\frac{1}{8}(2)+b$

$b+\frac{1}{4}=\frac{1}{4}$

b=0 .

We can then write the equation of the line: $y=\frac{1}{8}x$

Report an Error

Example Question #5 : How To Find The Equation Of A Parallel Line

Which of these formulas could be a formula for a line perpendicular to the line 2x + 3y = 16 ?

Possible Answers:

6y - 9x = 16.5

4x + 6y = 24

6y + 9x = 16

3y - 4x = 23

4y - 9x = 24

Correct answer:

6y - 9x = 16.5

Explanation:

This is a two-step problem. First, the slope of the original line needs to be found. The slope will be represented by "" when the line is in -intercept form (y=mx+b) .

2x +3y = 16

3y = -2x +16

$y = \left(\frac{-2}{3}\right)x +\left(\frac{16}{3}\right)$

So the slope of the original line is $-\frac{2}{3}$ . A line with perpendicular slope will have a slope that is the inverse reciprocal of the original. So in this case, the slope would be $\frac{3}{2}$ . The second step is finding which line will give you that slope. For the correct answer, we find the following:

6y - 9x = 16.5

6y = 9x +16.5

$y= \left(\frac{3}{2}x\right) +\left(\frac{16.5}{6}\right)$

So, the slope is $\frac{3}{2}$ , and this line is perpendicular to the original.

Report an Error

Example Question #21 : How To Find The Equation Of A Parallel Line

Find the equation of a line that goes through the point (0, 4) and is parallel to the line with the equation y=4x-2 .

Possible Answers:

y=4x-4

y=-4x+4

y=4x+4

$y=\frac{1}{4}x-4$

Correct answer:

y=4x+4

Explanation:

For lines to be parallel, they must have the same slope. The slope of the line we are looking for then must be .

The point that's given in the equation is also the y-intercept.

Using these two pieces of information, we know that the equation for the line must be y=4x+4

Report an Error

Example Question #1 : Coordinate Plane

There is a circle on a coordinate plain. Its perimeter passes through the point (1,0)

. At this point meets a tangent line, which also passes through the point (5,7)

. What is the slope of the line perpindicular to this tangent line?

Possible Answers:

$-\frac{4}{7}$

$\frac{7}{6}$

$\frac{4}{7}$

$-\frac{7}{4}$

$\frac{7}{4}$

Correct answer:

$-\frac{4}{7}$

Explanation:

In this kind of problem, it's important to keep track of information given about your line of interest. In this case, the coordinates given set up the stage for us to be able to get to our line of focus - the line perpendicular to the tangent line. In order to determine the perpendicular line's slope, the tangent line's slope must be calculated. Keeping in mind that:

$slope =\frac{rise}{run}=\frac{\Delta y}{\Delta x} =\frac{y_2-y_1}{x_2-x_1}$

where y2,x2 and y1,x1 are assigned arbitrarily as long as the order of assignment is maintained.

$\frac{y_2-y_1}{x_2-x_1}=\frac{7-0}{5-1}=\frac{7}{4}$ which is the slope of the tangent line.

To calculate the perpendicular line, we have to remember that the product of the tangent slope and the perpendicular slope will equal -1.

$\frac{7}{4} x \frac{?}{?} = -1$ , the perpendicular slope can then be calculated as $\frac{-4}{7}$

Report an Error

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View SSAT- Upper Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Boston, English Tutors in New York City, Algebra Tutors in Seattle, Reading Tutors in Houston, ISEE Tutors in Houston, SAT Tutors in New York City, SAT Tutors in Phoenix, SSAT Tutors in Los Angeles, Biology Tutors in Los Angeles, MCAT Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in Seattle, LSAT Courses & Classes in Atlanta, ACT Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in San Diego, GMAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Houston, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC, ACT Test Prep in Atlanta, ACT Test Prep in San Diego, MCAT Test Prep in Boston, SAT Test Prep in Atlanta, GRE Test Prep in Phoenix, SSAT Test Prep in Chicago, SSAT Test Prep in Seattle, ACT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #174 : Coordinate Geometry

Example Question #175 : Coordinate Geometry

Example Question #176 : Coordinate Geometry

Example Question #177 : Coordinate Geometry

Example Question #11 : How To Find The Equation Of A Parallel Line

Example Question #451 : Ssat Upper Level Quantitative (Math)

Example Question #181 : Coordinate Geometry

Example Question #5 : How To Find The Equation Of A Parallel Line

Example Question #21 : How To Find The Equation Of A Parallel Line

Example Question #1 : Coordinate Plane

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: