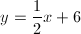Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Coordinate Geometry

What is the equation of a line that is parallel to 3x + 5y = 8 and passes through (10, 4) ?

Possible Answers:

$y=\frac{5}{6}x-10$

$y=\frac{3}{4}x-2$

$y=\frac{5}{3}x+5$

$y=-\frac{3}{5}x+10$

$y=\frac{3}{8}x-5$

Correct answer:

$y=-\frac{3}{5}x+10$

Explanation:

To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.

3x + 5y = 8

5y=-3x+8

$y=-\frac{3}{5}x+\frac{8}{5}$

The slope of the line will be $-\frac{3}{5}$ . In slope intercept-form, we know that the line will be $y=-\frac{3}{5}x+b$ . Now we can use the given point to find the y-intercept.

$y=-\frac{3}{5}x+b$

$4=-\frac{3}{5}(10)+b$

4=-6+b

10=b

The final equation for the line will be $y=-\frac{3}{5}x+10$ .

Report an Error

Example Question #3 : Coordinate Geometry

What line is parallel to 3x + 2y = 6 and passes through the point (2,-1) ?

Possible Answers:

$y = \frac{2}{3}x - 3$

$y = \frac{-3}{2}x + 2$

$y = \frac{-1}{3}x - 5$

y = 3x - 15

$y = \frac{1}{3}x + 6$

Correct answer:

$y = \frac{-3}{2}x + 2$

Explanation:

Start by converting the original equation to slop-intercept form.

3x + 2y = 6

2y=-3x+6

$y=-\frac{3}{2}+3$

The slope of this line is $-\frac{3}{2}$ . A parallel line will have the same slope. Now that we know the slope of our new line, we can use slope-intercept form and the given point to solve for the y-intercept.

$y=-\frac{3}{2}x+b$

$-1=-\frac{3}{2}(2)+b$

-1=-3+b

b=2

Plug the y-intercept into the slope-intercept equation to get the final answer.

$y=-\frac{3}{2}x+2$

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point (4, 2) ?

Possible Answers:

$\small y=\frac{1}{2}x+6$

$\small y=2x-6$

$\small y=\frac{1}{2}x$

$\small y=-2x+10$

Correct answer:

$\small y=\frac{1}{2}x$

Explanation:

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.

$\small 2=(\frac{1}{2})(4)+b$

$\small 2=2+b$

$\small b=0$

Therefore, the equation of the line is $\small y=\frac{1}{2}x$ .

Report an Error

Example Question #4 : Coordinate Geometry

What line is parallel to 5x + 3y = 8 , and passes through the point (6,-4) ?

Possible Answers:

$y = \frac{-5}{3}x + 6$

$y = \frac{3}{2}x - 4$

$y = \frac{-2}{3}x + 5$

$y = \frac{3}{5}x - 2$

$y = \frac{1}{3}x - 3$

Correct answer:

$y = \frac{-5}{3}x + 6$

Explanation:

Converting the given line to slope-intercept form we get the following equation:

$y = \frac{-5}{3}x + \frac{8}{3}$

For parallel lines, the slopes must be equal, so the slope of the new line must also be $\frac{-5}{3}$ . We can plug the new slope and the given point into the slope-intercept form to solve for the y-intercept of the new line.

y = mx + b

$-4 = \frac{-5}{3}(6) + b$

-4=-10+b

b = 6

Use the y-intercept in the slope-intercept equation to find the final answer.

$y = \frac{-5}{3}x + 6$

Report an Error

Example Question #3 : Coordinate Geometry

What line is parallel to 2x+3y=6 at (3, 2) ?

Possible Answers:

$y=-\frac{2}{3}x-4$

None of the answers are correct

$y=-\frac{2}{3}x+4$

$y=-\frac{3}{2}x+8$

$y=-\frac{3}{2}x+4$

Correct answer:

$y=-\frac{2}{3}x+4$

Explanation:

Find the slope of the given line: y=mx+b (slope intercept form)

$y=\frac{-2}{3}x+2$ therefore the slope is $\frac{-2}{3}$

Parallel lines have the same slope, so now we need to find the equation of a line with slope $\frac{-2}{3}$ and going through point (3, 2) by substituting values into the point-slope formula.

$2=\frac{-2}{3}(3)+b$

So, b=4

Thus, the new equation is $y=\frac{-2}{3}x+4$

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

If the line through the points (5, –3) and (–2, p) is parallel to the line y = –2x – 3, what is the value of p ?

Possible Answers:

–10

–17

Correct answer:

Explanation:

Since the lines are parallel, the slopes must be the same. Therefore, (p+3) divided by (–2–5) must equal –2. 11 is the only choice that makes that equation true. This can be solved by setting up the equation and solving for p, or by plugging in the other answer choices for p.

$\frac{p--3}{-2-5}=\frac{p+3}{-2-5}=-2$

$\frac{p+3}{-7}=-2$

$(\frac{p+3}{-7})-7=-2(-7)$

p+3=14

p=11

Report an Error

Example Question #171 : Coordinate Geometry

Find the equation of the line that goes through the point (-3, 1) and is parallel to the line with the equation y=2x-1 .

Possible Answers:

$y=-\frac{1}{2}x+7$

y=2x-3

y=-2x+7

y=2x+7

Correct answer:

y=2x+7

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

We can then plug in the given point and the slope into the equation of a line to find the y-intercept.

1=2(-3)+b

-6+b=1

b=7

Now, we can write the equation of the line.

y=2x+7

Report an Error

Example Question #172 : Coordinate Geometry

Find the equation of the line that passes through the point (1, -2) and is parallel to the line with the equation $y=\frac{3}{2}x-1$ .

Possible Answers:

$y=\frac{3}{2}x+\frac{7}{2}$

$y=-\frac{2}{3}x-\frac{7}{2}$

$y=\frac{3}{2}x-\frac{7}{2}$

$y=\frac{3}{2}x-\frac{1}{2}$

Correct answer:

$y=\frac{3}{2}x-\frac{7}{2}$

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be $\frac{3}{2}$ .

Now, we can plug in the point given by the question to find the y-intercept.

$-2=\frac{3}{2}(1)+b$

$b+\frac{3}{2}=-2$

$b=-\frac{7}{2}$

From this, we can write the following equation:

$y=\frac{3}{2}x-\frac{7}{2}$

Report an Error

Example Question #221 : Geometry

Find the equation of the line that passes through the point (-2, -4) and is parallel to the line with the equation y=3x-2 .

Possible Answers:

y=3x+2

$y=-\frac{1}{3}x+2$

y=-3x+2

$y=\frac{1}{3}x+2$

Correct answer:

y=3x+2

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

Next, plug in the point given by the question to find the y-intercept of the line.

-4=3(-2)+b

b-6=-4

b=2

Now, we know that the equation of the line must be y=3x+2 .

Report an Error

Example Question #171 : Lines

Find the equation of the line that passes through the point (1, 2) and is parallel to the line with the equation y=-2x-1 .

Possible Answers:

y=-2x+4

y=2x-3

$y=\frac{1}{2}x+4$

y=-2x-4

Correct answer:

y=-2x+4

Explanation:

Because the two lines are parallel, we know that the slope of the line we need to find must also be .

Next, plug in the point given by the question to find the y-intercept of the line.

2=-2(1)+b

b-2=2

b=4

Now, we know the equation of the line must be y=-2x+4 .

Report an Error

View SSAT- Upper Level Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

View SSAT- Upper Level Tutors

Crystal
Certified Tutor

SUNY at Binghamton, Bachelor of Science, Mechanical Engineering.

View SSAT- Upper Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Seattle, Statistics Tutors in Boston, Spanish Tutors in Washington DC, English Tutors in Washington DC, MCAT Tutors in Chicago, Reading Tutors in Philadelphia, Calculus Tutors in Chicago, Computer Science Tutors in San Diego, Chemistry Tutors in Los Angeles, Physics Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Boston, GMAT Courses & Classes in Miami, ISEE Courses & Classes in Atlanta, MCAT Courses & Classes in Atlanta, SSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Washington DC, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Boston, LSAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Atlanta, SAT Test Prep in Washington DC, LSAT Test Prep in Los Angeles, ISEE Test Prep in Denver, GMAT Test Prep in Miami, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Atlanta, GMAT Test Prep in Seattle, ISEE Test Prep in Miami, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : Geometry

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #2 : Coordinate Geometry

Example Question #3 : Coordinate Geometry

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #4 : Coordinate Geometry

Example Question #3 : Coordinate Geometry

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #171 : Coordinate Geometry

Example Question #172 : Coordinate Geometry

Example Question #221 : Geometry

Example Question #171 : Lines

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: