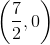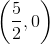All SSAT Upper Level Math Resources
Example Questions
Example Question #351 : Coordinate Geometry
Subtract 
The complex conjugate of a complex number 



Example Question #621 : Ssat Upper Level Quantitative (Math)
Give the product of 
The correct answer is not given among the other responses.
The correct answer is not given among the other responses.
The product of a complex number 

which will always be a real number. Therefore, all four given choices, all of which are imaginary, can be immediately eliminated. The correct response is that the correct answer is not given among the other responses.
Example Question #353 : Coordinate Geometry
Add 
The complex conjugate of a complex number 



Example Question #351 : Coordinate Geometry
Multiply the complex conjugate of 

The complex conjugate of a complex number 




Example Question #631 : Ssat Upper Level Quantitative (Math)
Multiply the complex conjugate of 8 by 
None of the other responses gives the correct product.
The complex conjugate of a complex number 




Example Question #411 : Geometry
Multiply the complex conjugate of 

None of the other responses gives the correct product.
The complex conjugate of a complex number 



Multiply this by 
Recall that by definition 
Example Question #21 : How To Graph Complex Numbers
Multiply the following complex numbers:
FOIL the product out:
To FOIL multiply the first terms from each binomial together, multiply the outer terms of both terms together, multiply the inner terms from both binomials together, and finally multiply the last terms from each binomial together.
Recall that i is an imaginary number and by definition 
Example Question #1 : How To Graph Inverse Variation
Give the equation of the vertical asymptote of the graph of the equation 
The vertical asymptote of an inverse variation function is the vertical line of the equation 





Example Question #2 : How To Graph Inverse Variation
Give the 

The graph has no 
The graph has no 
The 




This is identically false, so the graph has no 
Example Question #3 : How To Graph Inverse Variation
Give the 

The graph has no 
The 






Certified Tutor
All SSAT Upper Level Math Resources