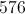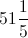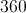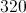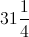Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Middle Level Math : Numbers and Operations

Study concepts, example questions & explanations for SSAT Middle Level Math

Create An Account

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2021 : Ssat Middle Level Quantitative (Math)

The sales tax for a given city is 8.5%. How much will someone shopping there pay for $139.34 worth of groceries, after tax is figured in?

Possible Answers:

$\$ 151.18$

$\$ 127.50$

$\$257.78$

$\$140.52$

$\$147.84$

Correct answer:

$\$ 151.18$

Explanation:

To calculate the tax, multiply 8.5%. or, equivalently, 0.085, by $139.34, rounding to the nearest cent:

$139.34 \cdot 0.085 \approx 11.84$

Add the tax to the price before tax:

139.34 +11.84 = 151.18

The amount paid will be $151.18.

Report an Error

Example Question #5 : Percentages

Exactly $\frac{1}{3}$ of the plants in a garden are tomato plants. Which of the following could be the total number of plants in the garden?

Possible Answers:

Correct answer:

Explanation:

The total number of plants has to be divisible by 3. Of the answer choices, the only one that is divisible by 3 is 18. You can check this because numbers that are divisible have the sum of their digits also divisible by 3. For example,

1 + 8 = 9

which is divisible by 3, so 18 is divisible by 3.

Report an Error

Example Question #561 : Arithmetic

330 is 75% of what number?

Possible Answers:

220

440

420

400

$247 \frac{1}{2}$

Correct answer:

440

Explanation:

330 is 75% of a number we will call ; alternatively, 0.75 multiplied by is equal to 330. Set up this equation and solve for :

0.75 N = 330

$0.75 N \div 0.75 = 330\div 0.75$

N = 440

Report an Error

Example Question #562 : Arithmetic

88 is $12 \frac{1}{2}$ % of what number?

Possible Answers:

576

704

Correct answer:

704

Explanation:

We can rewrite $12 \frac{1}{2}$ % as 12.5%. 88 is 12.5% of a number , or, equivalently, 0.125 multiplied by a number is equal to 88. We can write this as an equation and solve for :

0.125 N = 88

$0.125 N \div 0.125 = 88 \div 0.125$

N =704

Report an Error

Example Question #3 : How To Find The Whole From The Part With Percentage

32 is $2 \frac{1}{2}$ % of what number?

Possible Answers:

128

1,280

$7\frac{7}{8}$

800

$\frac{4}{5}$

Correct answer:

1,280

Explanation:

We can rewrite $2 \frac{1}{2}$ % as 2.5%. 32 is 2.5% of a number , or, equivalently, 0.025 multiplied by a number is equal to 32. We can write this as an equation and solve for :

0.025 N = 32

$0.025 N \div 0.025 = 32 \div 0.025$

N = 1,280

Report an Error

Example Question #5 : How To Work With Percentages

To get on the ballot for student body president, a student must turn in a petition with the signatures of 3% of the students. If there are 5,319 students, how many signatures must a student get to be on that ballot? (Nearest whole person)

Possible Answers:

1,596

106

160

220

1,064

Correct answer:

160

Explanation:

3% of 5,319 can be calculated by multiplying 5,319 by 0.03, the decimal equivalent of 3%:

$5,319 \times 0.03 = ?$

Multiply 5,319 by 3, then move the decimal point so that two digits are to the right:

$5,319 \times 3 =15,957$ ,

$5,319 \times 0.03 = 159.57$

Rounded to the nearest whole number, this is 160 signatures.

Report an Error

Example Question #571 : Arithmetic

3,200 is 160% of what number?

Possible Answers:

2,400

5,120

3,040

$2,133\frac{1}{3}$

2,000

Correct answer:

2,000

Explanation:

Set up the proportion statement and solve for by cross-multiplying:

$\frac{3,200}{N}= \frac{160}{100}$

$N \cdot 160 = 3,200 \cdot 100 = 320,000$

$N \cdot 160 \div 160 = 320,000\div 160$

N = 2,000

Report an Error

Example Question #572 : Arithmetic

12 is $\frac{3}{4} \%$ of what number?

Possible Answers:

900

1,600

$\frac{9}{100}$

Correct answer:

1,600

Explanation:

Set up the proportion statement and solve for by cross-multiplying:

$\frac{12}{N } = \frac{\frac{3}{4}}{100}$

$\frac{3}{4} \cdot N = 12 \cdot 100 = 1,200$

$\frac{4}{3} \cdot \frac{3}{4} \cdot N = \frac{4}{3} \cdot 1,200$

$N = \frac{4,800}{3} =1,600$

Report an Error

Example Question #1 : How To Find The Whole From The Part With Percentage

If 40 percent of a number is 44, what is 60 percent of the same number?

Possible Answers:

26.4

10.6

Correct answer:

Explanation:

To determine what 60 percent of the number is, one must first determine what the number is. To find the number, set up a proportion relating the original percentage and the value of the percentage where the top number is the fractional value and the bottom number is the total.

$\frac{Portion}{Total}=\frac{40 percent}{100 percent}=\frac{44}{number}$

Use cross multiplication to solve for the number.

Once the number is found, the new percentage can be found. There are two ways to do this: multiplication or a proportion.

Multiplication:
Proportion: $\frac{60percent}{100percent}=\frac{x}{110}$

This means that 60 percent of the number is 66.

Report an Error

Example Question #1361 : Numbers And Operations

128 is $40\%$ of what number?

Possible Answers:

$51 \frac{1}{5}$

320

360

$31\frac{1}{4}$

300

Correct answer:

320

Explanation:

128 is $40\%$ of a number we will call ; alternatively, 0.40 multiplied by is equal to 128 . Set up this equation and solve for :

0.4 N = 128

$0.4 N \div 0.4 = 128\div 0.4$

N= 320

Report an Error

View SSAT- Middle Level Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

View SSAT- Middle Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View SSAT- Middle Level Tutors

Meredith
Certified Tutor

University of Arkansas at Little Rock, Bachelor in Arts, English. University of Arkansas at Little Rock, Masters in Education...

All SSAT Middle Level Math Resources

10 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in Miami, SAT Tutors in Houston, MCAT Tutors in Atlanta, Physics Tutors in San Francisco-Bay Area, Biology Tutors in San Francisco-Bay Area, Computer Science Tutors in Denver, English Tutors in Washington DC, LSAT Tutors in Atlanta, Physics Tutors in Boston, Computer Science Tutors in Boston

Popular Courses & Classes

SAT Courses & Classes in Houston, MCAT Courses & Classes in Washington DC, SSAT Courses & Classes in Seattle, ACT Courses & Classes in Miami, GMAT Courses & Classes in Phoenix, MCAT Courses & Classes in Chicago, LSAT Courses & Classes in Chicago, SAT Courses & Classes in Phoenix, SSAT Courses & Classes in New York City, ISEE Courses & Classes in Los Angeles

Popular Test Prep

ACT Test Prep in Denver, MCAT Test Prep in Seattle, ACT Test Prep in San Diego, ISEE Test Prep in Denver, LSAT Test Prep in Seattle, SAT Test Prep in Denver, GRE Test Prep in Philadelphia, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Atlanta, MCAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Middle Level Math : Numbers and Operations

Study concepts, example questions & explanations for SSAT Middle Level Math

All SSAT Middle Level Math Resources

Example Questions

Example Question #2021 : Ssat Middle Level Quantitative (Math)

Example Question #5 : Percentages

Example Question #561 : Arithmetic

Example Question #562 : Arithmetic

Example Question #3 : How To Find The Whole From The Part With Percentage

Example Question #5 : How To Work With Percentages

Example Question #571 : Arithmetic

Example Question #572 : Arithmetic

Example Question #1 : How To Find The Whole From The Part With Percentage

Example Question #1361 : Numbers And Operations

All SSAT Middle Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: