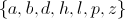All SSAT Middle Level Math Resources
Example Questions
Example Question #572 : Ssat Middle Level Quantitative (Math)
Define two sets as follows:
Which of the following is a subset of 
Each of the sets listed is a subset of 



A set is a subset of 







Example Question #1 : How To Find The Missing Part Of A List
Define two sets as follows:
Which of the following numbers is an element of 










425 and 565 are not multiples of 9; neither is in 




Example Question #2 : How To Find The Missing Part Of A List
Complete the set by determining the value of 
The set is composed of consecutive squares.
We can see that 
Therefore, 36 is the correct answer.
Example Question #3 : How To Find The Missing Part Of A List
Define sets 


How many elements are in the set 
One
The correct answer is not given among the other responses.
Three
Four
Two
The correct answer is not given among the other responses.
The elements of the set 







Example Question #4 : How To Find The Missing Part Of A List
Which of the following is a subset of the set

For a set to be a subset of 


We can do that with four choices:




However, the remaining set, 

Example Question #3 : Sets
Define sets 


How many elements are in the set 
Two
None
Three
The correct answer is not given among the other responses.
One
Three
The elements of the set 




Example Question #2 : How To Find The Missing Part Of A List
Which of the following is a subset of the set

The correct answer is not among the answer choices.
The correct answer is not among the answer choices.
We show that none of the four listed sets can be a subset of the primes by identifying one composite number in each - that is, by proving that there is at least one factor not equal to 1 or itself:




Since each set has at least one element that is not a prime, each has at least one element not in 

Example Question #2 : How To Find The Missing Part Of A List
How many of the following four numbers are elements of the set

(A)
(B)
(C)
(D)
None
Three
Four
Two
One
Three
By dividing the numerator of each fraction by its denominator, each fraction can be rewritten as its decimal equivalent:
All fractions except can be seen to fall between 0.3 and 0.4, exclusive. Three is the correct answer.
Note that 
Example Question #6 : How To Find The Missing Part Of A List
Define 
How many of the four sets listed are subsets of the set 
(A)
(B)
(C)
(D)
One
Three
Four
Two
None
Two
For a set to be a subset of 

In the sets 



However, 




The correct answer is therefore two.
Example Question #1 : Sets
What are the next two numbers of this sequence?
The sequence is formed by alternately adding 



Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources