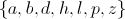All SSAT Middle Level Math Resources
Example Questions
Example Question #1 : Sets
Define two sets as follows:
Which of the following is a subset of ?
Each of the sets listed is a subset of .
is the union of and - that is, it is the set of all elements in one set or the other.
A set is a subset of if and only if every one of its elements is in . Three of the listed sets do not meet this criterion:
, , and , but none of those three elements are in . All of the elements in do appear in , however, so it is the subset.
Example Question #1 : Sets
Define two sets as follows:
Which of the following numbers is an element of ?
is the intersection of and - the set of all elements appearing in both sets. Thus, an element can be eliminated from by demonstrating either that it is not an element of or that it is not an element of .
is the set of positive integers ending in "5". 513 and 657 are not in , so they are not in .
is the set of muliples of 9. We test the three remaining numbers easily by seeing if 9 divides their digit sum:
425 and 565 are not multiples of 9; neither is in , so neither is in .
and , so . This is the correct choice.
Example Question #1 : How To Find The Missing Part Of A List
Complete the set by determining the value of .
The set is composed of consecutive squares.
We can see that will b equal to
Therefore, 36 is the correct answer.
Example Question #2 : Sets
Define sets and as follows:
How many elements are in the set ?
Four
Two
One
The correct answer is not given among the other responses.
Three
The correct answer is not given among the other responses.
The elements of the set - that is, the intersection of and - are exactly those in both sets. We can test each of the six elements in for inclusion in set by dividing each by 7 and noting which divisions yield no remainder:
and have no elements in common, so has zero elements. This is not one of the choices.
Example Question #2 : How To Find The Missing Part Of A List
Which of the following is a subset of the set
?
For a set to be a subset of , all of its elements must be elements of - that is, all of its elements must be multiples of 3. A set can therefore be proved to not be a subset of by identifying one element not a multiple of 3.
We can do that with four choices:
:
:
:
:
However, the remaining set, , can be demonstrated to include only multiples of 3:
is the correct choice.
Example Question #5 : How To Find The Missing Part Of A List
Define sets and as follows:
How many elements are in the set ?
One
The correct answer is not given among the other responses.
Two
None
Three
Three
The elements of the set - that is, the intersection of and - are exactly those in both sets. We can test each of the six elements in for inclusion in set by testing for divisibility by 5 - but this can be accomplished by looking at the last digit. Only 345, 600, and 855 have last digit 5 or 0 so only these three elements are divisible by 5. This makes three the correct answer.
Example Question #3 : How To Find The Missing Part Of A List
Which of the following is a subset of the set
?
The correct answer is not among the answer choices.
The correct answer is not among the answer choices.
We show that none of the four listed sets can be a subset of the primes by identifying one composite number in each - that is, by proving that there is at least one factor not equal to 1 or itself:
, so 25 has 5 as a factor, and 25 is not prime.
, so 9 has 3 as a factor, and 9 is not prime.
, so 21 has 3 and 7 as factors, and 21 is not prime.
, so 21 has 3 and 9 as factors, and 27 is not prime.
Since each set has at least one element that is not a prime, each has at least one element not in , and none of the sets are subsets of .
Example Question #581 : Ssat Middle Level Quantitative (Math)
How many of the following four numbers are elements of the set
?
(A)
(B)
(C)
(D)
Two
Three
None
Four
One
Three
By dividing the numerator of each fraction by its denominator, each fraction can be rewritten as its decimal equivalent:
All fractions except can be seen to fall between 0.3 and 0.4, exclusive. Three is the correct answer.
Note that is equal to 0.4, so we don't include it. The criterion requires strict inequality.
Example Question #6 : How To Find The Missing Part Of A List
Define .
How many of the four sets listed are subsets of the set ?
(A)
(B)
(C)
(D)
One
Three
Four
Two
None
Two
For a set to be a subset of , all of its elements must also be elements of - that is, all of its elements must be multiples of 5. An integer is a multiple of 5 if and only if its last digit is 5 or 0, so all we have to do is examine the last digit of each number in all four sets.
In the sets and , every element ends in a 5 or a 0, so all elements of both sets are in ; both sets are subsets of .
However, includes one element that does not end in either 5 or 0, namely 8934, so 8934 is not an element in ; subsequently, this set is not a subset of . Similarly, is not a subset of , since it includes 7472, which ends in neither 0 nor 5.
The correct answer is therefore two.
Example Question #581 : Ssat Middle Level Quantitative (Math)
What are the next two numbers of this sequence?
The sequence is formed by alternately adding and adding to each term to get the next term.
and are the next two numbers.
All SSAT Middle Level Math Resources