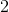SSAT Middle Level Math : Data Analysis
Study concepts, example questions & explanations for SSAT Middle Level Math
All SSAT Middle Level Math Resources
Example Questions
Example Question #25 : Tables
Mrs. Smith’s class made a line plot to show the amount of sugar that each student has in a given day.
How many students have 
Each X represents one person. There are 
Example Question #21 : Tables
Find 
If you are faced with a chart and a missing number, you need to figure out the pattern in the pairs that are shown.
If you think you have discovered the pattern, make sure to test it on each known pair and test if it is true for every pair.
The pattern will always stay the same. For these set of numbers the formula is
Therefore,
Example Question #215 : Data Analysis And Probability
The table below gives the number of students who scored in each of five ranges on a standardized test.
No student scored below 51.
What percent of the students scored 71 or better (nearest whole number)?
More information is needed to answer the question.
Add the numbers of students whose scores fell in the 71-80, 81-90, and 91-100 ranges:
Now add the number of students who took the test.
To find what percent 161 is of 241, evaluate:
67% of the students scored 71 or better.
Example Question #201 : Data Analysis
The line chart shows how many books each student in Mrs. Smith's class read this week. How many students are in Mrs. Smith's class?
In order to determine how many students there are we need to count up all the x marks above each number in the line chart, as each x represents one student. We know that 6 students read one book, 5 read two books, 6 read three books, 5 read four books, 5 read five books, and 3 read six books. 5 + 6 + 5 + 6 + 5 + 3 = 30, so the correct answer is 30.
Example Question #1 : Venn Diagrams
Using the Venn diagram shown above, what fraction represents the amount of students that enjoy both reading and playing video games?
The total number of survey respondents is equal to 
Thus, 
Example Question #2 : Venn Diagrams
The Venn diagram above, shows the results from a recent survey. The respondents were asked whether they enjoy playing video games, reading, or both. What percentage of the survey respondents enjoy both video games and reading?
The total number of survey respondents is equal to
Since the common part of the Venn diagram represents the respondents that enjoy both video games and reading, the solution is:
Example Question #633 : Ssat Middle Level Quantitative (Math)
The above Venn diagram depicts the number of students that: only play at the Rec. Center after school, only play at the park after school, and the students that play at both locations after school.
How many students play at both the park and Rec. Center after school?
To solve this problem, locate the common part of this Venn diagram. Since each of the two outside portions of the Venn diagram represent students that only play at either the park or Rec. Center.
The 
Example Question #634 : Ssat Middle Level Quantitative (Math)
Using the Venn diagram above, what fraction of the respondents play at both the Rec. Center and the park. (Keep in mind that the two outside portions of the Venn diagram represent respondents that only play at one location or the other).
To solve this problem, locate the common part of this Venn diagram. Since each of the two outside portions of the Venn diagram represent students that only play at either the park or Rec. Center. The 
This means that the total number of students (the denominator) must equal:
Making 
Example Question #635 : Ssat Middle Level Quantitative (Math)
The Venn diagram shown above represents the number of students that: only took math during summer school, only took social studies during summer school, and the number of students that took both math and social studies during summer school.
How many students took both math and social studies?
The common portion of this Venn diagram is equal to 
Example Question #636 : Ssat Middle Level Quantitative (Math)
What fraction of the above Venn diagram represents the number of students that took both math and social studies during summer school?
The common portion of this Venn diagram is equal to 
The denominator of the fraction is equal to the total number of students: \
Thus,
Certified Tutor
Certified Tutor
All SSAT Middle Level Math Resources
