We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Plane Geometry

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #142 : Triangles

The base angle of an isosceles triangle is $27^{\circ}$ . What is the vertex angle?

Possible Answers:

$126^{\circ}$

$108^{\circ}$

$149^{\circ}$

$75^{\circ}$

$135^{\circ}$

Correct answer:

$126^{\circ}$

Explanation:

Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.

Solve the equation $27+27+x=180$ for x to find the measure of the vertex angle.

x = 180 - 27 - 27

x = 126

Therefore the measure of the vertex angle is $126^{\circ}$ .

Report an Error

Example Question #143 : Triangles

An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?

Possible Answers:

4√3

3√3

Correct answer:

Explanation:

Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height². Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

Sat_math_167_01

Report an Error

Example Question #171 : Plane Geometry

Two sides of a triangle each have length 6. All of the following could be the length of the third side EXCEPT

Possible Answers:

Correct answer: 12

Explanation:

This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.

Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.

Report an Error

Example Question #146 : Triangles

A triangle has the following side lengths:

$13,\ 13, \textup{ and } 18$

Which of the following correctly describes the triangle?

Possible Answers:

None of these

Obtuse and scalene

Obtuse and isosceles

Acute and scalene

Acute and isosceles

Correct answer:

Acute and isosceles

Explanation:

The triangle has two sides of equal length, 13, so it is by definition isosceles.

To determine whether the triangle is acute, right, or obtuse, compare the sum of the squares of the lengths of the two shortest sides to the square of the length of the longest side. The former quantity is equal to

$13^{2} + 13^{2} = 169 + 169 = 338$

The latter quantity is equal to

$18^{2} = 324$

The former is greater than the latter; consequently, the triangle is acute. The correct response is that the triangle is acute and isosceles.

Report an Error

Example Question #1 : How To Find The Area Of A Trapezoid

A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?

Possible Answers:

$2\sqrt{2}$

$\sqrt{2}$

Correct answer:

Explanation:

In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:

area of trapezoid = (1/2)(4 + s)(s)

Similarly, the area of a square with sides of length a is given by a². Thus, the area of the square given in the problem is s².

We now can set the area of the trapezoid equal to the area of the square and solve for s.

(1/2)(4 + s)(s) = s²

Multiply both sides by 2 to eliminate the 1/2.

(4 + s)(s) = 2s²

Distribute the s on the left.

4s + s² = 2s²

Subtract s² from both sides.

4s = s²

Because s must be a positive number, we can divide both sides by s.

4 = s

This means the value of s must be 4.

The answer is 4.

Report an Error

Example Question #1 : Trapezoids

Find the area of a trapezoid given bases of length 1 and 2 and height of 2.

Possible Answers:

$\frac{3}{2}$

Correct answer:

Explanation:

To solve, simply use the formula for the area of a trapezoid. Thus,

$A=\frac{1}{2}(b1+b2)h=\frac{1}{2}(1+2)(2)=3$

Report an Error

Example Question #2 : Trapezoids

Square 1

The above figure shows Square ABCD . is the midpoint of $\overline{AB}$ ; is the midpoint of $\overline{CD}$ ; is the midpoint of $\overline{CN}$ . Construct $\overline{MO}$ .

If Square ABCD has area , what is the area of Quadrilateral AMOD ?

Possible Answers:

$\frac{1}{2} X$

$\frac{5}{8} X$

$\frac{\sqrt{17}}{4} X$

$\frac{\sqrt{17}}{2} X$

$\frac{3}{4} X$

Correct answer:

$\frac{5}{8} X$

Explanation:

Let be the common sidelength of the square. The area of the square is $X = t^{2}$ .

Construct segment $\overline{MN}$ . This divides the square into Rectangle AMND and a right triangle. The dimensions of Rectangle AMND are

AD = t

and

$ND = \frac{1}{2} CD = \frac{1}{2} t$ .

The area of Rectangle AMND s the product of these dimensions:

$A_{1} = AD \cdot ND = t \cdot \frac{1}{2} t = \frac{1}{2} t ^{2}$

The lengths of the legs of Right $\bigtriangleup MNO$ are

MN = AD = t

and

$NO = \frac{1}{2} CN = \frac{1}{2} \cdot \frac{1}{2} CD = \frac{1}{2} \cdot \frac{1}{2} t = \frac{1}{4} t$

The area of this right triangle is half the product of these lengths, or

$A_{2} = \frac{1}{2} \cdot MN \cdot NO = \frac{1}{2} \cdot t \cdot \frac{1}{4} t = \frac{1}{8} t ^{2}$

This is seen below:

Square 2

The sum of these areas is the area of Quadrilateral AMOD

$A = A_{1}+ A_{2}= t^{2}+\frac{1}{8}t ^{2} = \frac{5}{8} t ^{2}$ .

Substituting for $t^{2}$ , the area is $\frac{5}{8} X$ .

Report an Error

Example Question #3 : Quadrilaterals

Square 1

The above figure shows Square ABCD . is the midpoint of $\overline{AB}$ ; is the midpoint of $\overline{CD}$ ; is the midpoint of $\overline{CN}$ . Construct $\overline{MO}$ .

AM = t . Which of the following expresses the length of $\overline{MO}$ in terms of ?

Possible Answers:

$\frac{\sqrt{17}}{4} t$

$\frac{\sqrt{15}}{4} t$

$\frac{\sqrt{65}}{8} t$

$\frac{\sqrt{5}}{2} t$

$\frac{\sqrt{63}}{8} t$

Correct answer:

$\frac{\sqrt{17}}{4} t$

Explanation:

Construct $\overline{MN}$ as shown in the diagram below:

Square 1

Quadrilateral AMND is a rectangle, so opposite sides are congruent. Therefore, MN = AD = t .

Since is the midpoint of $\overline{CD}$ ,

$CN = \frac{1}{2} CD = \frac{1}{2} t$

Since is the midpoint of $\overline{CN}$ ,

$ON = \frac{1}{2} CN = \frac{1}{2} \cdot \frac{1}{2} t = \frac{1}{4} t$ .

$\bigtriangleup MNO$ is a right triangle, so, by the Pythagorean Theorem,

$MO = \sqrt{(MN)^{2}+(NO)^{2} }$

Substituting:

$MO= \sqrt{t^{2}+\left (\frac{1}{4}t \right)^{2} }$

$MO= \sqrt{t^{2}+ \frac {1}{16} t ^{2} }$

$MO= \sqrt{ \frac {17}{16} t ^{2} }$

Apply the Product of Radicals and Quotient of Radicals Rules:

$MO= \sqrt{ \frac {17}{16} t ^{2} }$

$= \sqrt{ \frac {17}{16} } \cdot \sqrt{t^{2}}$

$= \sqrt{ \frac {17}{16} } t$

$= \frac { \sqrt{17}}{ \sqrt{16}} \cdot t$

$= \frac { \sqrt{17}}{4} t$

Report an Error

Example Question #2 : Quadrilaterals

ABCD is a parallelogram. BD = 5. The angles of triangle ABD are all equal. What is the perimeter of the parallelogram?

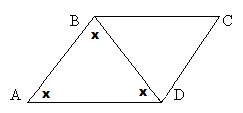
Figure_1

Possible Answers:

$15\sqrt{3}$

$10\sqrt{3}$

$11\sqrt{2}$

Correct answer:

Explanation:

If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.

We now have two equilateral triangles, so all sides of the triangles will be equal.

All sides therefore equal 5.

5+5+5+5 = 20

Report an Error

Example Question #1 : How To Find The Area Of A Parallelogram

Find the area of a parallelogram with length 6 and height 5.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the area of a parallelogram. Thus,

A=lh=5*6=30

Don't let a parallelogram fool you. It is just like a rectangle but on a slant. As long as you are given the height, and not the slant side length, you can use the same formula.

Report an Error

View SAT Mathematics Tutors

Patricia
Certified Tutor

Hofstra University, Bachelor in Arts, Clinical Psychology. CUNY Hunter College, Master of Science, Dance Therapy.

View SAT Mathematics Tutors

Troy
Certified Tutor

Rice University, Bachelor in Arts, Kinesiology.

View SAT Mathematics Tutors

Pavan
Certified Tutor

University of Connecticut, Bachelor in Arts, Statistics.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, GRE Courses & Classes in Los Angeles, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in Philadelphia, SAT Courses & Classes in Atlanta, Spanish Courses & Classes in Miami, MCAT Courses & Classes in Atlanta, ISEE Courses & Classes in Boston, GRE Courses & Classes in Washington DC, ACT Courses & Classes in Philadelphia

Popular Test Prep

LSAT Test Prep in Philadelphia, GRE Test Prep in San Diego, SSAT Test Prep in Washington DC, SAT Test Prep in Denver, ISEE Test Prep in Chicago, GRE Test Prep in Los Angeles, LSAT Test Prep in Los Angeles, SSAT Test Prep in Houston, ACT Test Prep in Denver, ISEE Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Plane Geometry

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #142 : Triangles

Example Question #143 : Triangles

Example Question #171 : Plane Geometry

Example Question #146 : Triangles

Example Question #1 : How To Find The Area Of A Trapezoid

Example Question #1 : Trapezoids

Example Question #2 : Trapezoids

Example Question #3 : Quadrilaterals

Example Question #2 : Quadrilaterals

Example Question #1 : How To Find The Area Of A Parallelogram

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: