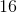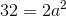The sum of the lengths of 2 sides of a triangle must be greater than—but not equal to—the length of the third side. Further, the third side must be longer than the difference between the greater and the lesser of the other two sides; therefore, 20 is the only possible answer.

Rule - the length of one side of a triangle must be greater than the differnce and less than the sum of the lengths of the other two sides.

Given lengths of two of the sides of the are 15 and 5. The length of the third side must be greater than 15-5 or 10 and less than 15+5 or 20.

The question asks what is the least possible integer length of BC, which would be 11

The set of possible lengths is: 7-4 < x < 7+4, or 3 < X < 11.

According to the Triangle Inequality Theorem, the sums of the lengths of any two sides of a triangle must be greater than the length of the third side. Since 10 + 8 is 18, the only length out of the answer choices that is not possible is 19.

Given two angles of unequal measure in a triangle, the side opposite the greater angle is longer than the side opposite the other angle. Therefore, we seek to find the relationship among the measures of the angles.

, and the measures of the interior angles of a triangle total , so

Since , 

, 

and, similarly, 

Therefore, 

, 

and the lengths of their opposite sides rank similarly:

.

The correct response is that only (II) can be true.

Given two angles of unequal measure in a triangle, the side opposite the greater angle is longer than the side opposite the other angle.

If  were the angle of greatest measure, then , and

.

Since the measures of the angles must total ,  cannot have the greatest measure.

, so we can explore two other possibilities:

, which here is possible if, for example, 

 and  - since ; and,

, which here is possible if, for example, 

 and  - since .

If , then ; if , then .

This makes the correct response II or III only.

In order for three lengths to represent the sides of a triangle, they must pass the Triangle Inequality. 

This means that the sum of any two sides of the triangle must exceed the length of the third side. 

With the given answers, the one set of lengths that fail this test is . 

Therefore, the lengths  could not represent the sides of a triangle. 

An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).

The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).

5 + 5 + 6 = 16

If we divide the square into two triangles via its diagonal, then we know that the length of the diagonal is equal to the length of the triangles' hypotenuse. 

We can use the Pythagorean Theorem to find the length of the two sides of one of our triangles. 

Since we're dealing with a square, we know that the two sides of the square (which are the same as the two sides of one of our triangles) will be equal to one another. Therefore, we can say: 

Now, solve for the unknown:

. 

This means that the length of the sides of our triangle, as well as the sides of our square, is . 

To find the area of the square, do the following:

.