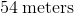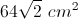SAT Math : Plane Geometry
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #2 : How To Find The Perimeter Of A Rectangle
Find the perimeter of a rectangle with width 6 and length 9.
To solve, simply use the formula for the perimeter.
Another way to solve this problem is to add up all of the sides. Remember that even though only two values are given, a rectangle has 4 sides. Thus,
Example Question #1 : How To Find The Perimeter Of A Rectangle
You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?
You have a poster of one of your favorite bands that you are planning on putting up in your dorm room. If the poster is 3 feet tall by 1.5 feet wide, what is the perimeter of the poster?
Perimeter of a rectangle is found via:
Example Question #3 : How To Find The Perimeter Of A Rectangle
Three of the vertices of a rectangle on the coordinate plane are located at the origin, 
The rectangle in question is below:
The lengths of the rectangle is 10, the distance from the origin to 
Example Question #211 : Plane Geometry
A rectangular garden has an area of 
We define the variables as 
We substitute these values into the equation for the area of a rectangle and get 
Lengths cannot be negative, so the only correct answer is 
Therefore, 
Example Question #1 : Squares
ABCD and EFGH are squares such that the perimeter of ABCD is 3 times that of EFGH. If the area of EFGH is 25, what is the area of ABCD?
15
5
225
75
25
225
Assign variables such that
One side of ABCD = a
and One side of EFGH = e
Note that all sides are the same in a square. Since the perimeter is the sum of all sides, according to the question:
4a = 3 x 4e = 12e or a = 3e
From that area of EFGH is 25,
e x e = 25 so e = 5
Substitute a = 3e so a = 15
We aren’t done. Since we were asked for the area of ABCD, this is a x a = 225.
Example Question #2 : Squares
A square has an area of 36. If all sides are doubled in value, what is the new area?
48
144
132
108
72
144
Let S be the original side length. S*S would represent the original area. Doubling the side length would give you 2S*2S, simplifying to 4*(S*S), giving a new area of 4x the original, or 144.
Example Question #2 : How To Find The Area Of A Square
Freddie is building a square pen for his pig. He plans to buy x feet of fencing to build the pen. This will result in a pen with an area of p square feet. Unfortunately, he only has enough money to buy one third of the planned amount of fencing. Which expression represents the area of the pen he can build with this limited amount of fencing?
9p
p/6
p/9
3p
p/3
p/9
If Freddie uses x feet of fencing makes a square, each side must be x/4 feet long. The area of this square is (x/4)2 = x2/16 = p square feet.
If Freddie uses one third of x feet of fencing makes a square, each side must be x/12 feet long. The area of this square is (x/12)2 = x2/144 = 1/9(x2/16) = 1/9(p) = p/9 square feet.
Alternate method:
The scale factor between the small perimeter and the larger perimeter = 1 : 3. Since we're comparing area, a two-dimensional measurement, we can square the scale factor and see that the ratio of the areas is 12 : 32 = 1 : 9.
Example Question #212 : Plane Geometry
If the diagonal of a square measures 
This is an isosceles right triangle, so the diagonal must equal 
Example Question #212 : Geometry
A square 
The area of 
Example Question #1 : How To Find The Area Of A Square
The perimeter of a square is 
The perimeter of a square is given by 
So the area of the new square is given by 
All SAT Math Resources
