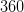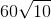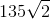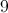All SAT Math Resources
Example Questions
Example Question #11 : Geometry
Assume l and m are parallel horizontal lines where l is above m. A third straight line k intersects both lines l and m, creating a total of 4 different angles on each of the two intersections. The intersections of lines l and m contain angles a, b, c, d and w, x, y, z, respectively. The angle layouts start with a and w in the top left position with the other angles following in alphabetical order in the clockwise direction. What is the degree value of angle z if angle c has a value of 67 degrees?






The purpose of this question is to understand the process of using geometry to find degree values of angles.
Since l and m are parallel lines, the respective angles on both lines will have equivalent degree values. This means that a and w, b and x, and so on will be the same degree amount. A straight line is 180 degrees, so you know that angle d is 
Example Question #2062 : Hspt Mathematics
Angle 


What is the measure of 

Let's begin by observing the larger angle. 








Example Question #1 : How To Find The Length Of The Side Of A Pentagon

The above diagram shows a pentagonal track with perimeter one third of a mile. Adrianne starts at Point A and runs clockwise until she gets halfway between Points D and E. Which of the following choices is closest to the number of feet she runs?
1,200 feet
1,000 feet
1,100 feet
1,300 feet
1,400 feet
1,200 feet
The perimeter of the pentagonal track is one third of a mile; one mile is equal to 5,280 feet, so the perimeter is

Each side of the pentagon has length one fifth of its perimeter, or

Adrianne runs three and one half sides, or

This makes 1,200 feet the closest, and correct, choice.
Example Question #1 : Pentagons

Aristotle High School has an unusual track in that it is shaped like a regular pentagon. Each side of the pentagon measures 264 feet.
Benny runs at a steady speed of eight miles an hour for ten minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Point D
Point C
Point A
Point B
Point E
Point C
Benny runs at a rate of eight miles an hour for ten minutes, or 


One mile comprises 5,280 feet, so this is equal to

Since each side of the track measures 264 feet, this means that Benny runs

This means Benny runs around the track for 25 sidelengths, which is 5 complete times, back to Point A; he then runs one more complete sidelength to Point B; and, finally, he runs 
Example Question #1 : How To Find An Angle In A Pentagon
Find the sum of all the angles in a pentagon.
To solve, simply use the formula to find the total degrees in a polygon, where n is thenumber of vertices.
In this particular case, a pentagon is a shape that has five sides and thus has five vertices.
Thus,
Example Question #1 : Hexagons

Archimedes High School has an unusual track in that it is shaped like a regular hexagon, as above. Each side of the hexagon measures 264 feet.
Alvin runs at a steady speed of seven miles an hour for twelve minutes, starting at point A and working his way clockwise. When he is finished, which of the following points is he closest to?
Point D
Point F
Point E
Point B
Point C
Point E
Alvin runs at a rate of seven miles an hour for twelve minutes, or 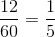


One mile comprises 5,280 feet, so this is equal to
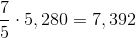
Since each side of the track measures 264 feet, this means that Alvin runs


which means that Alvin runs around the track four complete times, plus four more sides of the track. Alvin stops when he is at Point E.
Example Question #17 : Geometry
A circle with circumference 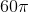
None of these
Below is the figure referenced; note that the hexagon is divided by its diameters, and that an apothem—a perpendicular bisector from the center to one side—has been drawn.

The circle has circumference 



The hexagon is divided into six equilateral triangles. One, 








this makes the perimeter of the hexagon six times this, or

Example Question #1 : Hexagons
How many diagonals are there in a regular hexagon?
A diagonal is a line segment joining two non-adjacent vertices of a polygon. A regular hexagon has six sides and six vertices. One vertex has three diagonals, so a hexagon would have three diagonals times six vertices, or 18 diagonals. Divide this number by 2 to account for duplicate diagonals between two vertices. The formula for the number of vertices in a polygon is:
where 
Example Question #1 : Hexagons
How many diagonals are there in a regular hexagon?
3
6
9
18
10
9
A diagonal connects two non-consecutive vertices of a polygon. A hexagon has six sides. There are 3 diagonals from a single vertex, and there are 6 vertices on a hexagon, which suggests there would be 18 diagonals in a hexagon. However, we must divide by two as half of the diagonals are common to the same vertices. Thus there are 9 unique diagonals in a hexagon. The formula for the number of diagonals of a polygon is:
where n = the number of sides in the polygon.
Thus a pentagon thas 5 diagonals. An octagon has 20 diagonals.
Example Question #19 : Geometry
Hexagon 



Below is the referenced hexagon, with some additional segments constructed.

Note that the segments 














and
For the same reason, 
By the Pythagorean Theorem,

Certified Tutor
Certified Tutor
All SAT Math Resources