All SAT II Math II Resources
Example Questions
Example Question #1 : Vectors
Add the vectors:
Combine the values as one vector.
Combine the terms.
The answer is:
Example Question #122 : Mathematical Relationships
Add in modulo 9:
In modulo 9 arithmetic, a number is congruent to the remainder of its division by 9.
Since
and


making "5" the correct response.
Example Question #121 : Mathematical Relationships



If 


To the nearest whole number, evaluate 


Insufficient information is given to answer the question.




Alternatively,
We can substitute the initial conditions for thevariables on the left side and the final conditions for those on the right side, then solve for 
Example Question #151 : Sat Subject Test In Math Ii



If 


Evaluate 







Alternatively stated,

We can substitute the initial conditions for the variables on the left side and the final conditions for those on the right side, then solve for 
Example Question #125 : Mathematical Relationships
![3\sqrt[4] {a} -5 \sqrt[4] {b} = 34](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827699/gif.latex)
Evaluate 
The system has no solution.
Rewrite the two equations by setting ![x = \sqrt [4] {a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827700/gif.latex)
![y = \sqrt [4] {b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827701/gif.latex)
![3\sqrt[4] {a} -5 \sqrt[4] {b} = 34](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827703/gif.latex)
The result is a two-by-two linear system in terms of 

This can be solved, among other ways, using Gaussian elimination on an augmented matrix:
Perform row operations until the left two columns show identity matrix 


![\sqrt [4] {a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827704/gif.latex)

Certified Tutor
Certified Tutor
All SAT II Math II Resources




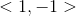


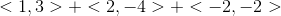
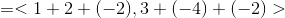
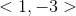
























![4 \sqrt[4] {a}+ 7 \sqrt[4] {b} =18](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827698/gif.latex)




![4 \sqrt[4] {a}+ 7 \sqrt[4] {b} =18](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827702/gif.latex)

















![\sqrt [4] {a} = 8](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827706/gif.latex)
![(\sqrt [4] {a}) ^{4}= 8^{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/827707/gif.latex)




