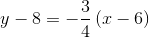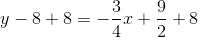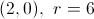Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Solving Piecewise And Recusive Functions

Define two functions as follows:

$f(x) = \begin{Bmatrix} 2x- 7& \textrm{for } x < 0 \\ & \\ 3x+ 3& \textrm{for } x\ge 0 \end{matrix}$

$g(x) = \begin{Bmatrix} 3x+ 3 & \textrm{for } x < 0 \\ & \\ 2x- 7 & \textrm{for } x\ge 0 \end{matrix}$

Evaluate $(f \circ g) (5)$ .

Possible Answers:

Correct answer:

Explanation:

By definition, $(f \circ g) (5) = f \left [ g (5) \right ]$

First, evaluate g(5) , using the definition of g(x) for nonnegative values of . Substituting for 5:

g(x) = 2x-7

$g(5) = 2\cdot 5 -7= 10 -7 = 3$

$(f \circ g) (5) = f \left [ g (5) \right ] = f(3)$ ; evaluate this using the definition of f(x) for nonnegative values of :

f(x) = 3x+ 3

$f(3) = 3 \cdot 3+ 3 = 9 + 3 = 12$

12 is the correct value.

Report an Error

Example Question #4 : Solving Piecewise And Recusive Functions

Which of the following would be a valid alternative definition for the provided function?

$f(x) = \left | \frac{3}{4} x - \frac{7}{3} \right |$

Possible Answers:

None of these

$f(x) = \left\{\begin{matrix} - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x < \frac{28}{9}\\ \\ \frac{3}{4} x - \frac{7}{3}& \textrm{for }x \ge \frac{28}{9} \end{matrix}\right.$

$f(x) = \left\{\begin{matrix} \frac{3}{4} x - \frac{7}{3} & \textrm{for }x < \frac{28}{9}\\ \\ - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x \ge \frac{28}{9} \end{matrix}\right.$

$f(x) = \left\{\begin{matrix} - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x < -\frac{28}{9}\\ \\ \frac{3}{4} x - \frac{7}{3}& \textrm{for }x \ge - \frac{28}{9} \end{matrix}\right.$

$f(x) = \left\{\begin{matrix} \frac{3}{4} x - \frac{7}{3} & \textrm{for }x < - \frac{28}{9}\\ \\ - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x \ge - \frac{28}{9} \end{matrix}\right.$

Correct answer:

$f(x) = \left\{\begin{matrix} - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x < \frac{28}{9}\\ \\ \frac{3}{4} x - \frac{7}{3}& \textrm{for }x \ge \frac{28}{9} \end{matrix}\right.$

Explanation:

The absolute value of an expression | a | is defined as follows:

| a | = a for $a \ge 0$

| a | = -a for a < 0

Therefore,

$f(x) = \left | \frac{3}{4} x - \frac{7}{3} \right | = \frac{3}{4} x - \frac{7}{3}$

if and only if

$\frac{3}{4} x - \frac{7}{3} \ge 0$ .

Solving this condition for :

$\frac{3}{4} x - \frac{7}{3} + \frac{7}{3} \ge 0 + \frac{7}{3}$

$\frac{3}{4} x \ge \frac{7}{3}$

$\frac{4}{3} \cdot \frac{3}{4} x \ge \frac{4}{3} \cdot \frac{7}{3}$

$x \ge \frac{28}{9}$

Therefore, $f(x) = \frac{3}{4} x - \frac{7}{3}$ for $x \ge \frac{28}{9}$ .

Similarly,

$f(x) = - \left (\frac{3}{4} x - \frac{7}{3} \right ) = - \frac{3}{4} x + \frac{7}{3}$ for $x < \frac{28}{9}$ .

The correct response is therefore

$f(x) = \left\{\begin{matrix} - \frac{3}{4} x + \frac{7}{3} & \textrm{for }x < \frac{28}{9}\\ \\ \frac{3}{4} x - \frac{7}{3}& \textrm{for }x \ge \frac{28}{9} \end{matrix}\right.$

Report an Error

Example Question #71 : Functions And Graphs

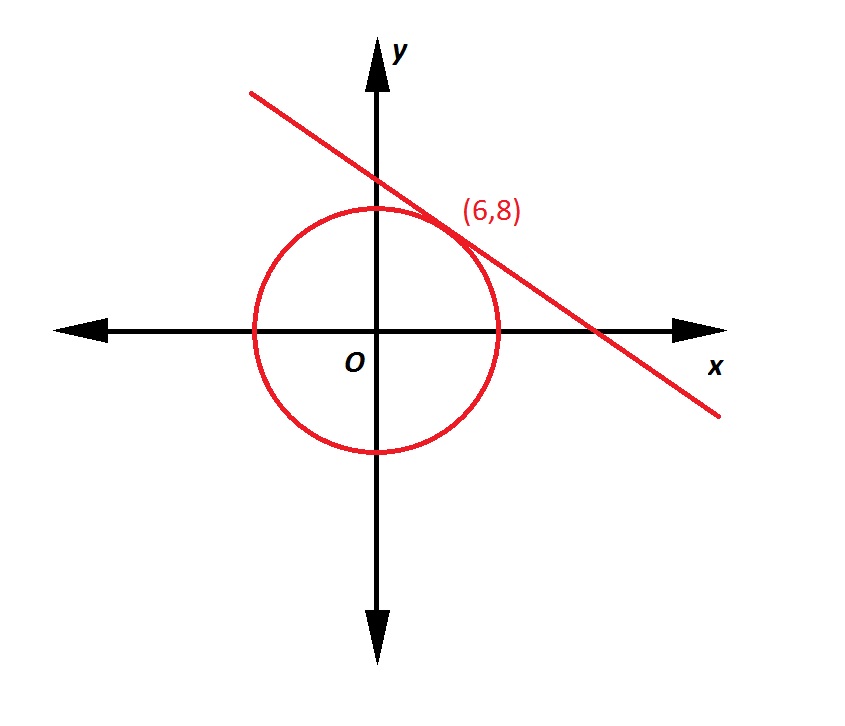
Circle

Note: Figure NOT drawn to scale.

Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?

Possible Answers:

$y = \frac{3}{4} x+ \frac{7}{2}$

$y = \frac{4}{3} x$

Insufficient information is given to determine the equation of the line.

$y = - \frac{4}{3} x+ 16$

$y = - \frac{3}{4} x+ \frac{25}{2}$

Correct answer:

$y = - \frac{3}{4} x+ \frac{25}{2}$

Explanation:

A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints (0,0),(6,8) , has slope

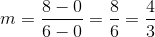
$m = \frac{8-0}{6-0} = \frac{8}{6} = \frac{4}{3}$ .

The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be $-\frac{3}{4}$ . Since it includes point (6,8) , we can use the point-slope form of the line to find its equation:

$y - y_{1} = m(x-x_{1})$

$y - 8= - \frac{3}{}4\left ( x-6 \right )$

$y - 8= - \frac{3}{4} x+ \frac{9}{2}$

$y - 8+ 8 = - \frac{3}{4} x+ \frac{9}{2} + 8$

$y = - \frac{3}{4} x+ \frac{25}{2}$

Report an Error

Example Question #1 : Conic Sections

What is the center and radius of the circle indicated by the equation?

(x-2)^2+y^2=36

Possible Answers:

$(2,0),\ r=6$

$(-2,0),\ r=36$

$(2,0),\ r=36$

$(-2,0),\ r=6$

Correct answer:

$(2,0),\ r=6$

Explanation:

A circle is defined by an equation in the format (x-h)^2+(y-k)^2=r^2 .

The center is indicated by the point (h,k) and the radius .

In the equation 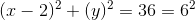(x-2)^2+(y)^2=36=6^2 , the center is (2,0) and the radius is .

Report an Error

Example Question #72 : Functions And Graphs

Give the axis of symmetry of the parabola of the equation

$f(x) = 3x^{2} + 9x - 16$

Possible Answers:

$x= \frac{1}{6}$

x = - 16

$x = -\frac{3}{2}$

$x = \frac{3}{2}$

$x= -\frac{1}{6}$

Correct answer:

$x = -\frac{3}{2}$

Explanation:

The line of symmetry of the parabola of the equation

$f(x) = ax^{2}+ bx + c$

is the vertical line

$x = -\frac{b}{2a}$

Substitute a = 3, b = 9 :

The line of symmetry is

$x = -\frac{9}{2 \cdot 3} = - \frac{9}{6} = -\frac{3}{2}$

That is, the line of the equation $x =- \frac{3}{2}$ .

Report an Error

Example Question #1 : Graphing Functions

Give the -coordinate of the vertex of the parabola of the function

$f(x) = 4x^{2}- 16x + 1$

Possible Answers:

129

Correct answer:

Explanation:

The -coordinate of the vertex of a parabola of the form

$f(x) = ax^{2}+ bx + c$

$x= -\frac{b}{2a}$ .

Substitute a= 4, b = -16 :

$x= -\frac{-16}{2\cdot 4} = -\frac{-16}{8} = 2$

The -coordinate is therefore f(2) :

$f(x) = 4x^{2}- 16x + 1$

$f(2) = 4 \cdot 2 ^{2}- 16 \cdot 2 + 1$

$f(2) = 4 \cdot 4- 16 \cdot 2 + 1$

f(2) = 16 - 32 + 1

f(2) = -15

Report an Error

Example Question #1 : Graphing Quadratic Functions And Conic Sections

A baseball is thrown straight up with an initial speed of 60 miles per hour by a man standing on the roof of a 100-foot high building. The height of the baseball in feet is modeled by the function

$h(t) = -16t^{2}+60t + 100$

To the nearest foot, how high is the baseball when it reaches the highest point of its path?

Possible Answers:

$132\textrm{ ft}$

$156 \textrm{ ft}$

$172\textrm{ ft}$

$120\textrm{ ft}$

$140\textrm{ ft}$

Correct answer:

$156 \textrm{ ft}$

Explanation:

We are seeking the value of when the graph of $h\left ( t\right )$ - a parabola - reaches its vertex.

To find this value, we first find the value of . For a parabola of the equation

$f\left ( t\right ) = at^{2}+ bt + c$ ,

the value of the vertex is

$t = -\frac{b}{2a}$ .

Substitute a = -16, b = 60 :

$t = -\frac{60}{2 (-16)} = 1.875$

The height of the baseball after 1.875 seconds will be

$h(1.875) = -16 \cdot 1.875^{2}+60 \cdot 1.875 + 100$

$h(1.875) = -56.25 +112.5 + 100 \approx 156$ feet.

Report an Error

Example Question #1 : Graphing Quadratic Functions And Conic Sections

Give the -coordinate of the vertex of the parabola of the function

$f(x) = 2x^{2} + 6x + 5$ .

Possible Answers:

$\frac{37}{2}$

$\frac{1}{2}$

$\frac{3}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

The -coordinate of the vertex of a parabola of the form

$f(x) = ax^{2}+ bx + c$

$x= -\frac{b}{2a}$ .

Set a = 2, b = 6 :

$x= -\frac{6}{2\cdot 2} = -\frac{6}{4} =- \frac{3}{2}$

The -coordinate is therefore $f\left (- \frac{3}{2} \right )$ :

$f(x) = 2x^{2} + 6x + 5$

$f \left ( -\frac{3}{2} \right )= 2\left ( -\frac{3}{2} \right )^{2}+ 6\left ( -\frac{3}{2} \right ) + 5$

$= 2\left ( \frac{9}{4} \right ) + 6\left (- \frac{3}{2} \right ) + 5$

$= \frac{9}{2} - 9 + 5 = \frac{1}{2}$ , which is the correct choice.

Report an Error

Example Question #1 : Graphing Quadratic Functions And Conic Sections

A baseball is thrown upward from the top of a one hundred and fifty-foot-high building. The initial speed of the ball is forty-five miles per hour. The height of the ball after seconds is modeled by the function

$h (t) = -16t^{2}+ 45t +150$

How high does the ball get (nearest foot)?

Possible Answers:

$182 \textrm{ ft}$

$205 \textrm{ ft}$

$195 \textrm{ ft}$

$173 \textrm{ ft}$

$166 \textrm{ ft}$

Correct answer:

$182 \textrm{ ft}$

Explanation:

A quadratic function such as has a parabola as its graph. The high point of the parabola - the vertex - is what we are looking for.

The vertex of a function

$h (t) = at^{2}+bt +c$

has as coordinates

$\left ( - \frac{b}{2a} , h \left ( - \frac{b}{2a} \right ) \right )$ .

The second coordinate is the height and we are looking for this quantity. Since $h (t) = -16t^{2}+ 45t +150$ , setting a = -16, b= 45 :

$- \frac{b}{2a} = - \frac{45}{2(-16)} = \frac{45}{32} = 1.40625$ seconds for the ball to reach the peak.

The height of the ball at this point is h ( 1.40625 ) , which can be evaluated by substitution:

$h (t) = -16t^{2}+ 45t +150$

$h (1.40625 ) = -16 (1.40625 )^{2}+ 45 (1.40625 ) +150$

$\approx -16 (1.9775 ) + 45 (1.40625 ) +150$

$\approx -31.6406 + 63.2813 + 150$

$\approx 181.6407$

Round this to 182 feet.

Report an Error

Example Question #74 : Functions And Graphs

Give the -intercept(s) of the parabola of the equation

$f(x) = 3x^{2}-9x -54$

Possible Answers:

(-4,0) and (9,0)

$\left ( -\frac{3}{2}, 0 \right )$ and $\left ( \frac{3}{2}, 0 \right )$

(-54,0)

(-3,0) and (6,0)

The parabola has no -intercept.

Correct answer:

(-3,0) and (6,0)

Explanation:

Set f(x)= 0 and solve for :

$f(x) = 3x^{2}-9x -54$

$3x^{2}-9x -54 = 0$

The terms have a GCF of 2, so

$3\left ( x^{2}- 3x - 18 \right )= 0$

The trinomial in parentheses can be FOILed out by noting that -6 +3 = -3 and $-6 \times 3= -18$ :

3(x-6)(x+3)=0

And you can divide both sides by 3 to get rid of the coefficient:

(x-6)(x+3)=0

Set each of the linear binomials to 0 and solve for :

$x - 6 = 0 \Rightarrow x = 6$

$x +3= 0 \Rightarrow x = -3$

The parabola has as its two intercepts the points (-3,0) and (6,0) .

Report an Error

View SAT Subject Test in Mathematics Level 2 Tutors

Kevin
Certified Tutor

Duke University, Bachelor of Science, Economics.

View SAT Subject Test in Mathematics Level 2 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View SAT Subject Test in Mathematics Level 2 Tutors

Irina
Certified Tutor

New York University, Bachelors, Biochemistry.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Philadelphia, GRE Tutors in Denver, English Tutors in Atlanta, Computer Science Tutors in Dallas Fort Worth, SSAT Tutors in Boston, Calculus Tutors in Phoenix, Spanish Tutors in San Francisco-Bay Area, Math Tutors in Washington DC, SSAT Tutors in San Francisco-Bay Area, MCAT Tutors in Miami

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City, LSAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Los Angeles, LSAT Courses & Classes in San Diego, LSAT Courses & Classes in New York City, MCAT Courses & Classes in Seattle, Spanish Courses & Classes in New York City, ISEE Courses & Classes in Boston, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Miami, LSAT Test Prep in New York City, ISEE Test Prep in Denver, ACT Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC, LSAT Test Prep in Washington DC, MCAT Test Prep in Denver, GRE Test Prep in Phoenix, GMAT Test Prep in Atlanta, MCAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #3 : Solving Piecewise And Recusive Functions

Example Question #4 : Solving Piecewise And Recusive Functions

Example Question #71 : Functions And Graphs

Example Question #1 : Conic Sections

Example Question #72 : Functions And Graphs

Example Question #1 : Graphing Functions

Example Question #1 : Graphing Quadratic Functions And Conic Sections

Example Question #1 : Graphing Quadratic Functions And Conic Sections

Example Question #1 : Graphing Quadratic Functions And Conic Sections

Example Question #74 : Functions And Graphs

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: