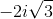We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math II : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math II

Create An Account

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

Example Question #1 : Other Properties

Define the functions and on the set of real numbers as follows:

$f (x) = \sqrt{x- 16}$

$g(x) = \sqrt{x- 4}$

Give the natural domain of the composite function $f \circ g$ .

Possible Answers:

$[16, \infty)$

$[32, \infty)$

$[4, \infty)$

$[260, \infty)$

$[0 , \infty)$

Correct answer:

$[260, \infty)$

Explanation:

The natural domain of the composite function $f \circ g$ is defined to be the intersection of the two sets.

One set is the natural domain of . Since is defined to be the square root of an expression, the radicand must be nonnegative. Therefore,

$x - 4 \geq 0$

$x \geq 4$

This set is $[4, \infty)$ .

The other set is the set of numbers that the function pairs with a number within the domain of . Since the radicand of the square root in must be nonnegative,

$x - 16 \geq 0$

$x \geq 16$

For g(x) to fall within this set:

$g(x) \geq 16$

$\sqrt{x- 4} \geq 16$

$x - 4 \geq 256$

$x \geq 260$

This set is $[260, \infty)$ .

$[4, \infty) \cap [260, \infty) = [260, \infty)$ , which is the natural domain.

Report an Error

Example Question #1 : Solving Functions

If f(x) = (3x+5)^2 , what must f(-2) be?

Possible Answers:

121

Correct answer:

Explanation:

Replace the value of negative two with the x-variable.

There is no need to use the FOIL method to expand the binomial.

f(-2) = (3(-2)+5)^2 = (-6+5)^2 = (-1)^2 = 1

The answer is:

Report an Error

Example Question #1 : Solving Linear Functions

Let f(x) = -3x+9 . What is the value of $f(\frac{7}{8})$ ?

Possible Answers:

$\frac{51}{4}$

$\frac{17}{3}$

$\frac{51}{8}$

$\frac{17}{2}$

Correct answer:

$\frac{51}{8}$

Explanation:

Substitute the fraction as .

$f(\frac{7}{8}) = -3(\frac{7}{8})+9$

Multiply the whole number with the numerator.

$\frac{-21}{8}+9$

Convert the expression so that both terms have similar denominators.

$-\frac{21}{8}+\frac{9(8)}{1(8)} = -\frac{21}{8}+\frac{72}{8}$

The answer is: $\frac{51}{8}$

Report an Error

Example Question #51 : Functions And Graphs

If f(x) = 5 , what must f(10) be?

Possible Answers:

Correct answer:

Explanation:

A function of x equals five. This can be translated to:

y=5

This means that every point on the x-axis has a y value of five.

Therefore, f(10) =5 .

The answer is:

Report an Error

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Rewrite as a single logarithmic expression:

$\ln (y+ 1) - \ln (y + 2) + \ln (y + 3)$

Possible Answers:

$= \ln \frac{y^{2}+4y + 3}{y + 2}$

$\ln \frac{y^{2}+3}{y + 2}$

$\ln \left (y + 2 \right )$

$= \ln \frac{y+1}{y^{2}+5y+6}$

$\ln \left (y + 4 \right )$

Correct answer:

$= \ln \frac{y^{2}+4y + 3}{y + 2}$

Explanation:

Using the properties of logarithms

$\ln a - \ln b = \ln \frac{a}{b}$ and $\ln a + \ln b = \ln ab$ ,

simplify as follows:

$\ln (y+ 1) - \ln (y + 2) + \ln (y + 3)$

$= \ln \frac{y+ 1}{y + 2} + \ln (y + 3)$

$= \ln \left [\frac{y+ 1}{y + 2} \cdot (y + 3) \right ]$

$= \ln \frac{y^{2}+4y + 3}{y + 2}$

Report an Error

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Simplify by rationalizing the denominator:

$\frac{11}{6- \sqrt{3}}$

Possible Answers:

$2+ \sqrt{3}$

$\frac{6+ \sqrt{3}}{3 }$

$\frac{6- \sqrt{3}}{3 }$

$\frac{11\sqrt{3}}{3}$

$2- \sqrt{3}$

Correct answer:

$\frac{6+ \sqrt{3}}{3 }$

Explanation:

Multiply the numerator and the denominator by the conjugate of the denominator, which is $6 + \sqrt{3}$ . Then take advantage of the distributive properties and the difference of squares pattern:

$\frac{11}{6- \sqrt{3}}$

$= \frac{11(6+ \sqrt{3})}{\left (6- \sqrt{3} \right )(6+ \sqrt{3})}$

$= \frac{11(6+ \sqrt{3})}{ 6^{2}- \left (\sqrt{3} \right ) ^{2}\right }$

$= \frac{11(6+ \sqrt{3})}{36-3 }$

$= \frac{11(6+ \sqrt{3})}{3 3 }$

$= \frac{6+ \sqrt{3}}{3 }$

Report an Error

Example Question #3 : Solving Exponential, Logarithmic, And Radical Functions

Simplify:

$\sqrt[3]{\sqrt[2]{x^{-9}}}$

You may assume that is a nonnegative real number.

Possible Answers:

$\frac{ \sqrt{x}}{x^{2}}$

$\frac{1}{x^{3}}$

$x \sqrt{x}$

$\sqrt[3]{x}$

$\frac{ \sqrt[3]{x}}{x }$

Correct answer:

$\frac{ \sqrt{x}}{x^{2}}$

Explanation:

The best way to simplify a radical within a radical is to rewrite each root as a fractional exponent, then convert back.

First, rewrite the roots as exponents.

$\sqrt[3]{\sqrt[2]{x^{-9}}} = \sqrt[3]{\left ( x^{-9} \right ) ^{\frac{1}{2}} } = \left ( \left ( x^{-9} \right ) ^{\frac{1}{2}} \right )^{\frac{1}{3}} = x ^{-9 \cdot \frac{1}{2} \cdot \frac{1}{3}} } } = x ^{- \frac{3}{2} } }= \frac{1}{x^{\frac{3}{2}}}$

Then convert back to a radical and rationalizing the denominator:

$\frac{1}{x^{\frac{3}{2}}} = \frac{1}{\sqrt {x^{3}}} = \frac{1 \cdot \sqrt{x}}{\sqrt {x^{3} \cdot \sqrt{x}}} = \frac{ \sqrt{x}}{\sqrt {x^{4} }} =\frac{ \sqrt{x}}{x^{2}}$

Report an Error

Example Question #4 : Solving Exponential, Logarithmic, And Radical Functions

Let $f(x) = 2^{x}+ 3^{2x}$ . What is the value of f(-2) ?

Possible Answers:

$\frac{1}{85}$

$\frac{85}{324}$

$\textup{The answer is not given.}$

Correct answer:

$\frac{85}{324}$

Explanation:

Replace the integer as .

$f(-2) = 2^{-2}+ 3^{2(-2)} = 2^{-2}+ 3^{-4}$

Evaluate each negative exponent.

$2^{-2} = \frac{1}{2^2} = \frac{1}{4}$

$3^{-4} = \frac{1}{3^4} = \frac{1}{81}$

Sum the fractions.

$\frac{1}{4}+\frac{1}{81} = \frac{1(81)}{4(81)}+\frac{1(4)}{81(4)} = \frac{85}{324}$

The answer is: $\frac{85}{324}$

Report an Error

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Find : $\sqrt{-3x-5} = 7$

Possible Answers:

Correct answer:

Explanation:

Square both sides to eliminate the radical.

$(\sqrt{-3x-5}) ^2= 7^2$

-3x-5 = 49

Add five on both sides.

-3x-5 +5= 49+5

-3x = 54

Divide by negative three on both sides.

$\frac{-3x}{-3} = \frac{54}{-3}$

The answer is:

Report an Error

Example Question #1 : Solving Functions

If $f(x) = 2\sqrt{x}-\sqrt{x-3}$ , what is the value of f(-3) ?

Possible Answers:

$2i\sqrt3 -i\sqrt6$

-12i

$i\sqrt6$

$-2i\sqrt3$

Correct answer:

$2i\sqrt3 -i\sqrt6$

Explanation:

Substitute the value of negative three as .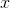

$f(-3) = 2\sqrt{-3}-\sqrt{(-3)-3}$

$2\sqrt{-3}-\sqrt{-6} = 2\sqrt{-1}\cdot \sqrt{3} - \sqrt{-1}\cdot \sqrt{6}$

The terms will be imaginary. We can factor out an 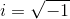$i = \sqrt{-1}$ out of the right side. Replace them with .

The answer is: $2i\sqrt3 -i\sqrt6$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

View SAT Subject Test in Mathematics Level 2 Tutors

Luu Chi Hieu
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science.

View SAT Subject Test in Mathematics Level 2 Tutors

Antonia
Certified Tutor

University of Michigan-Ann Arbor, Bachelor of Engineering, Nuclear Engineering. University of Wisconsin-Madison, Current Grad...

View SAT Subject Test in Mathematics Level 2 Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

All SAT II Math II Resources

2 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Boston, Algebra Tutors in Seattle, Math Tutors in Atlanta, Algebra Tutors in Dallas Fort Worth, Reading Tutors in Houston, Statistics Tutors in Chicago, SSAT Tutors in Atlanta, Calculus Tutors in Denver, ISEE Tutors in Washington DC, French Tutors in Los Angeles

Popular Courses & Classes

Spanish Courses & Classes in Houston, SSAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Miami, SAT Courses & Classes in San Diego, ACT Courses & Classes in New York City, GRE Courses & Classes in New York City, SAT Courses & Classes in Washington DC, ACT Courses & Classes in Washington DC, Spanish Courses & Classes in Boston, SSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

ACT Test Prep in Washington DC, ISEE Test Prep in Chicago, MCAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Atlanta, ISEE Test Prep in Phoenix, MCAT Test Prep in Houston, GRE Test Prep in New York City, ISEE Test Prep in New York City, SSAT Test Prep in Dallas Fort Worth, SAT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math II : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math II

All SAT II Math II Resources

Example Questions

Example Question #1 : Other Properties

Example Question #1 : Solving Functions

Example Question #1 : Solving Linear Functions

Example Question #51 : Functions And Graphs

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Example Question #3 : Solving Exponential, Logarithmic, And Radical Functions

Example Question #4 : Solving Exponential, Logarithmic, And Radical Functions

Example Question #1 : Solving Exponential, Logarithmic, And Radical Functions

Example Question #1 : Solving Functions

All SAT II Math II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: