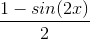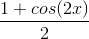SAT II Math I : SAT Subject Test in Math I
Study concepts, example questions & explanations for SAT II Math I
All SAT II Math I Resources
Example Questions
Example Question #1 : Trigonometric Identities
Which of the following is equivalent to: 
We can multiply the bottom with its conjugate and obtain:
Then we can use the pythagorean identity for the cosines and sines:
Finally, we can split the fractions up and translate them into the trigonometric identity:
Alternatively, you could take this and other answer choices and work the opposite way by translating all of the trigonometric ratios into sines and cosines, using the identities.
Another potential option is to try certain angle values for the original identity and selecting the choice that most closely matches the answer choices when the same angle is substituted (although one must beware of where the function(s) are undefined).
Example Question #11 : Trigonometric Identities
Simplify 
The power-reducing formulas state that:
Example Question #1 : Mean
Tom recieved an 87%, 92%, 77%, and 90% on his 4 exams. Find the mean of these scores.
86.5%
87%
85%
86%
86.5%
To find the mean of a certain set of numbers we need to add all enteries together and then divide by how many numbers you have.
In our case we do:
Example Question #2 : Mean
Karen wants to get an average of 92% at the end of the semester in her class. She has 1 test left to take before the semester is over to raise her average. If she recieved an 88%, 87%, 95%, and 93% on her tests what does she need to recieve on her last test to obtain the 92% average?
93%
95%
100%
97%
97%
For this question we need to set up an equation to find the mean, set it equal to our desired mean of 92 and solve for our missing test value.
From here we perform algebraic procedures to simplify the equation
Example Question #3 : Mean
Clara recieved 10 apples on Monday, 9 apples on Tuesday, and 5 apples on Wednesday. What was the average number of apples she recieved?
To solve this problem we use the equation to find the mean. We add all entries and then divide by the number of entries we have. It is as follows:
Example Question #4 : Mean
On her past five tests, Julie scored 
The mean is the same as the average. To find the mean, use the following formula:
Example Question #1 : Mean
The following stem and leaf plot illustrates the number of baseball cards owned by a group of friends. What is the average number of baseball cards that each individual owns?
First, write out the individual values found within this stem and leaf plot to figure out how many values there are.
Now, finding the mean is the same as finding the average. Recall how to find the average:
Thus, the mean number of baseball cards owned is found by the following:
Example Question #5 : Mean
In order for Michael to get a "B" in his trigonometry class, he needs to have an average of 
Recall how to find the average of a set of numbers:
Now, let 
Now, solve for 
Example Question #4 : Mean
The average temperature for a city is given by the following graph.
What is the average temperature for the months of May-September?
First, figure out the temperatures.
May:
June:
July:
August:
September:
Now, recall how to find the mean of a set of numbers:
Example Question #6 : Mean
The mean of 
Recall how to find the mean:
Certified Tutor
All SAT II Math I Resources
