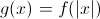A reflection over the line  involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).

The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:

The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so

When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a). 

Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2). 

Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.

First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x₁, y₁) and (x₂, y₂).

slope = (2 – (–4))/(–6 –3)

= 6/–9 = –2/3

Next, we can use the point-slope formula to find the equation for q.

y – y₁ = slope(x – x₁)

y – 2 = (–2/3)(x – (–6))

Multiply both sides by 3.

3(y – 2) = –2(x + 6)

3y – 6 = –2x – 12

Add 2x to both sides.

2x + 3y – 6 = –12

Add six to both sides.

2x + 3y = –6

The answer is 2x + 3y = –6.

This quadratic is presented in vertex form. 

First, the negative sign will reflect the graph over the x-axis, if the negative sign were inside the parentheses it would be reflected over the y-axis. 

Second, the 2 will stretch the graph vertically, if the 2 had been inside the parentheses that would have been a horizontal shrink. 

Third, the 5 inside the parentheses, translates the graph 5 spaces right because we are plugging in a positive 5 into the original vertex form for "h". A negative 5 would change the sign inside the parentheses. 

Finally, the 4 outside the parentheses is the k-value, which translates the graph up 4 spaces in this case. 

If the function is reflected over the x-axis, then .

It will be the opposite of what is currently written.

Therefore, 

becomes 

.

When a function is reflected over the y-axis, . 

becomes 

which is simplifed as 

.

In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding. 

Therefore, g(x) = f(–x).

f(x) = x³ – 2x² + x – 4

g(x) = f(–x) = (–x)³ – 2(–x)² + (–x) + 4

g(x) = (–1)³x³ –2(–1)²x² – x + 4

g(x) = –x³ –2x² –x + 4.

The answer is –x³ –2x² –x + 4.

The period is the time it takes for the graph to complete one cycle.

In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches .

Therefore, the period is 

When we reflect a point across the line, , we swap the x- and y-coordinates; therefore, in each point, we will switch the x and y-coordinates: 

 becomes , 

 becomes , and 

 becomes . 

The correct answer is the following:

The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.