All PSAT Math Resources
Example Questions
Example Question #1 : How To Find An Angle In A Hexagon
If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?
The sum of the interior angles of a polygon is given by 

Example Question #1 : How To Find An Angle In A Hexagon
In a rectangular hexagon, what is the meaure of each interior angle?
72 degrees
90 degrees
150 degrees
105 degrees
120 degrees
120 degrees
The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures
Example Question #4 : How To Find An Angle In A Hexagon

Note:Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Example Question #5 : How To Find An Angle In A Hexagon

Note: Figure NOT drawn to scale.
Refer to the above figure. Evaluate 
The sum of the degree measures of the angles of a (six-sided) hexagon, is
We can solve for 
Example Question #6 : How To Find An Angle In A Hexagon
Three angles of a hexagon measure 
This hexagon cannot exist.
The sum of the degree measures of the angles of a (six-sided) hexagon, is
Let 

Example Question #7 : How To Find An Angle In A Hexagon
What is the measurement of one of the interior angles of a regular hexagon?
To find the sum of the interior angles of any regular polygon, use the formula 

The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):
The measurement of one angle in a regular hexagon is 120 degrees.
Example Question #21 : Plane Geometry
Calculate the approximate area a regular hexagon with the following side length:
Cannot be determined
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the given problem we know that the side length of a regular hexagon is the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Round the answer to the nearest whole number.
Certified Tutor
Certified Tutor
All PSAT Math Resources














































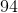











![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)










