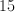We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Coordinate Geometry

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : Plane Geometry

A student creates a challenge for his friend. He first draws a square, the adds the line for each of the 2 diagonals. Finally, he asks his friend to draw the circle that has the most intersections possible.

How many intersections will this circle have?

Possible Answers:

Correct answer:

Explanation:

Report an Error

Example Question #1 : Geometry

Two pairs of parallel lines intersect:

Screen_shot_2013-03-18_at_10.29.11_pm

If A = 135^o, what is 2*|B-C| = ?

Possible Answers:

170°

160°

150°

180°

140°

Correct answer:

180°

Explanation:

By properties of parallel lines A+B = 180^o, B = 45^o, C = A = 135^o, so 2*|B-C| = 2* |45-135| = 180^o

Report an Error

Example Question #181 : Coordinate Geometry

Lines and are parallel. $\angle HFC=10^{\circ}$ , $\angle DGI=50^{\circ}$ , $\triangle EFG$ is a right triangle, and $\overline{EG}$ has a length of 10. What is the length of $\overline{EF}$

Possible Answers:

Not enough information.

Correct answer:

Explanation:

Since we know opposite angles are equal, it follows that angle $\angle AFE=10^{\circ}$ and $\angle BGE=50^{\circ}$ .

Imagine a parallel line passing through point . The imaginary line would make opposite angles with $\angle AFE$ & $\angle BGE$ , the sum of which would equal $\angle FEG$ . Therefore, $\angle FEG=60^{\circ}$ .

$\cos (60)=.5=\frac{EG}{EF}\rightarrow EF=\frac{EG}{.5}=20$

Report an Error

Example Question #11 : How To Find An Angle Of A Line

If $\angle A$ measures $(40-10x)^{\circ}$ , which of the following is equivalent to the measure of the supplement of $\angle A$ ?

Possible Answers:

$(10x+50)^{\circ}$

$(50-10x)^{\circ}$

$(140-10x)^{\circ}$

$(100x)^{\circ}$

$(10x+140)^{\circ}$

Correct answer:

$(10x+140)^{\circ}$

Explanation:

When the measure of an angle is added to the measure of its supplement, the result is always 180 degrees. Put differently, two angles are said to be supplementary if the sum of their measures is 180 degrees. For example, two angles whose measures are 50 degrees and 130 degrees are supplementary, because the sum of 50 and 130 degrees is 180 degrees. We can thus write the following equation:

$\dpi{100} measure\ of\ \angle A+ measure\ of\ supplement\ of\ \angle A=180$

$\dpi{100} 40-10x+ measure\ of\ supplement\ of\ \angle A=180$

Subtract 40 from both sides.

$\dpi{100} -10x+ measure\ of\ supplement\ of\ \angle A=140$

Add $\dpi{100} 10x$ to both sides.

$\dpi{100} measure\ of\ supplement\ of\ \angle A=140+10x=10x+140$

The answer is $(10x+140)^{\circ}$ .

Report an Error

Example Question #182 : Coordinate Geometry

In the following diagram, lines and are parallel to each other. What is the value for ?

Sat_math_166_03

Possible Answers:

It cannot be determined

80^o

100^o

60^o

30^o

Correct answer:

80^o

Explanation:

When two parallel lines are intersected by another line, the sum of the measures of the interior angles on the same side of the line is 180°. Therefore, the sum of the angle that is labeled as 100° and angle y is 180°. As a result, angle y is 80°.

Another property of two parallel lines that are intersected by a third line is that the corresponding angles are congruent. So, the measurement of angle x is equal to the measurement of angle y, which is 80°.

Report an Error

Example Question #183 : Coordinate Geometry

The measure of the supplement of angle A is 40 degrees larger than twice the measure of the complement of angle A. What is the sum, in degrees, of the measures of the supplement and complement of angle A?

Possible Answers:

190

140

Correct answer:

190

Explanation:

Let A represent the measure, in degrees, of angle A. By definition, the sum of the measures of A and its complement is 90 degrees. We can write the following equation to determine an expression for the measure of the complement of angle A.

A + measure of complement of A = 90

Subtract A from both sides.

measure of complement of A = 90 – A

Similarly, because the sum of the measures of angle A and its supplement is 180 degrees, we can represent the measure of the supplement of A as 180 – A.

The problem states that the measure of the supplement of A is 40 degrees larger than twice the measure of the complement of A. We can write this as 2(90-A) + 40.

Next, we must set the two expressions 180 – A and 2(90 – A) + 40 equal to one another and solve for A:

180 – A = 2(90 – A) + 40

Distribute the 2:

180 - A = 180 – 2A + 40

Add 2A to both sides:

180 + A = 180 + 40

Subtract 180 from both sides:

A = 40

Therefore the measure of angle A is 40 degrees.

The question asks us to find the sum of the measures of the supplement and complement of A. The measure of the supplement of A is 180 – A = 180 – 40 = 140 degrees. Similarly, the measure of the complement of A is 90 – 40 = 50 degrees.

The sum of these two is 140 + 50 = 190 degrees.

Report an Error

Example Question #242 : New Sat Math Calculator

$\dpi{100} \small \overline{AB}$ is a straight line. $\dpi{100} \small \overline{CD}$ intersects $\dpi{100} \small \overline{AB}$ at point $\dpi{100} \small E$ . If $\dpi{100} \small \angle AEC$ measures 120 degrees, what must be the measure of $\dpi{100} \small \angle BEC$ ?

Possible Answers:

$\dpi{100} \small 75$ degrees

None of the other answers

$\dpi{100} \small 70$ degrees

$\dpi{100} \small 60$ degrees

$\dpi{100} \small 65$ degrees

Correct answer:

$\dpi{100} \small 60$ degrees

Explanation:

$\dpi{100} \small \angle AEC$ & $\dpi{100} \small \angle BEC$ must add up to 180 degrees. So, if $\dpi{100} \small \angle AEC$ is 120, $\dpi{100} \small \angle BEC$ (the supplementary angle) must equal 60, for a total of 180.

Report an Error

Example Question #11 : Plane Geometry

Two parallel lines are intersected by a transversal. If the minor angle of intersection between the first parallel line and the transversal is $36^{\circ}$ , what is the minor angle of intersection between the second parallel line and the transversal?

Possible Answers:

$18^{\circ}$

$66^{\circ}$

$54^{\circ}$

$144^{\circ}$

$36^{\circ}$

Correct answer:

$36^{\circ}$

Explanation:

When a line intersects two parallel lines as a transversal, it always passes through both at identical angles (regardless of distance or length of arc).

Report an Error

Example Question #11 : Geometry

If $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ , $\overline{BE}\perp \overleftrightarrow{GC}$ , and $m\angle HGC=58^\circ$ , what is the measure, in degrees, of $\angle ABE$ ?

Alternate interior angles

Possible Answers:

122

148

Correct answer:

148

Explanation:

The question states that $\overleftrightarrow{FH} \parallel \overleftrightarrow{AD}$ . The alternate interior angle theorem states that if two parallel lines are cut by a transversal, then pairs of alternate interior angles are congruent; therefore, we know the following measure:

$m\angle GCA = 58^\circ$

The sum of angles of a triangle is equal to 180 degrees. The question states that $\overline{BE}\perp \overleftrightarrow{GC}$ ; therefore we know the following measure:

$m \angle BEC = 90^\circ$

Use this information to solve for the missing angle: $\angle EBC$

$180^\circ=m\angle EBC+58^\circ+90^\circ$

$m\angle EBC=32^\circ$

The degree measure of a straight line is 180 degrees; therefore, we can write the following equation:

$180^\circ=m\angle ABE+32^\circ$

$m\angle ABE=148^\circ$

The measure of $\angle ABE$ is 148 degrees.

Report an Error

Example Question #2 : How To Find An Angle Of A Line

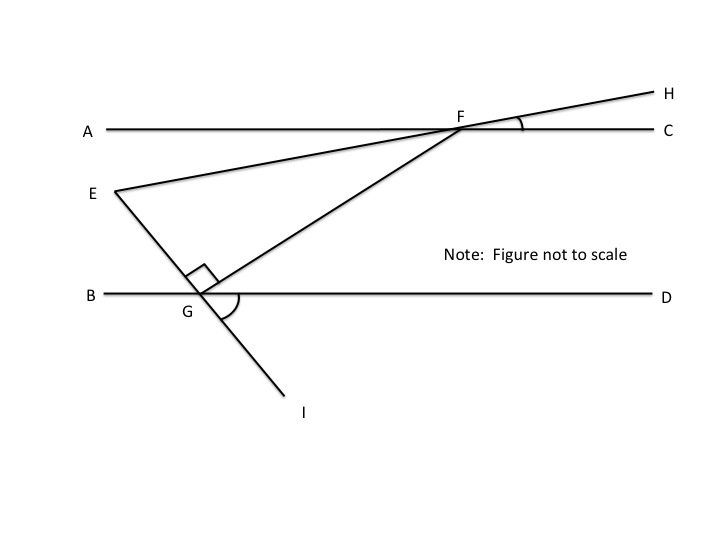
Lines A and B in the diagram below are parallel. The triangle at the bottom of the figure is an isosceles triangle.

Act2

What is the degree measure of angle ?

Possible Answers:

Correct answer:

Explanation:

Since A and B are parallel, and the triangle is isosceles, we can use the supplementary rule for the two angles, and 2x+30 which will sum up to 180 . Setting up an algebraic equation for this, we get 4x+2x+30=180 . Solving for , we get x=25 . With this, we can get either 2(25)+30=80 (for the smaller angle) or 4(25)=100 (for the larger angle - must then use supplementary rule again for inner smaller angle). Either way, we find that the inner angles at the top are 80 degrees each. Since the sum of the angles within a triangle must equal 180, we can set up the equation as 80+80+y=180

y=20 degrees.

Report an Error

View PSAT Mathematics Tutors

Dejuan
Certified Tutor

University of Illinois at Urbana-Champaign, Bachelor of Science, Electrical Engineering.

View PSAT Mathematics Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View PSAT Mathematics Tutors

Mohammad
Certified Tutor

Rutgers University-New Brunswick, Bachelor of Science, Mathematics. Rutgers University-New Brunswick, Master of Science, Stat...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in San Diego, French Tutors in Dallas Fort Worth, Reading Tutors in Philadelphia, Computer Science Tutors in Los Angeles, Computer Science Tutors in Phoenix, SAT Tutors in Dallas Fort Worth, Biology Tutors in San Francisco-Bay Area, SAT Tutors in Chicago, SSAT Tutors in Phoenix, GMAT Tutors in Chicago

Popular Courses & Classes

SAT Courses & Classes in Boston, Spanish Courses & Classes in Phoenix, GMAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Los Angeles, ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Denver, ISEE Courses & Classes in New York City, LSAT Courses & Classes in Denver, Spanish Courses & Classes in Chicago, SAT Courses & Classes in New York City

Popular Test Prep

GRE Test Prep in Los Angeles, SAT Test Prep in Denver, LSAT Test Prep in Miami, ISEE Test Prep in San Diego, LSAT Test Prep in Houston, GRE Test Prep in Houston, GRE Test Prep in Atlanta, ISEE Test Prep in New York City, GMAT Test Prep in Boston, GMAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Coordinate Geometry

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #3 : Plane Geometry

Example Question #1 : Geometry

Example Question #181 : Coordinate Geometry

Example Question #11 : How To Find An Angle Of A Line

Example Question #182 : Coordinate Geometry

Example Question #183 : Coordinate Geometry

Example Question #242 : New Sat Math Calculator

Example Question #11 : Plane Geometry

Example Question #11 : Geometry

Example Question #2 : How To Find An Angle Of A Line

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: