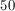All PSAT Math Resources
Example Questions
Example Question #2 : How To Solve For A Variable As Part Of A Fraction
If 

3/38
none of these
38/3
9/114
7/12
38/3
cross multiply:
(6)(19) = 9x
114=9x
x = 38/3
Example Question #3 : How To Solve For A Variable As Part Of A Fraction
Find x.
None
Cross multiply:
Example Question #1 : How To Solve For A Variable As Part Of A Fraction
The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.
Let numerator = N and denominator = D.
According to the first statement,
N = (D x 5) + 4.
According to the second statement, N / 2 = 3 * D.
Let's multiply the second equation by –2 and add itthe first equation:
–N = –6D
+[N = (D x 5) + 4]
=
–6D + (D x 5) + 4 = 0
–1D + 4 = 0
D = 4
Thus, N = 24.
Therefore, N/D = 24/4 = 6.
Example Question #11 : How To Solve For A Variable As Part Of A Fraction
Solve for 
Solve for 
Step 1: Cross-multiply to eliminate the fraction
Step 2: Solve for 
Example Question #1 : Describing Roles Of Variables And Constants
Hannah is selling candles for a school fundraiser all fall. She sets a goal of selling 




The number of weeks that she has sold candles this month.
The number of candles she has remaining for the month.
The number of candles that she has sold thus far that week.
The number of candles that she sells each week.
The number of candles that she sells each week.
Since we know that 


Example Question #1 : Translating Words To Linear Equations
We have three dogs: Joule, Newton, and Toby. Joule is three years older than twice Newton's age. Newton is Toby's age younger than eleven years. Toby is one year younger than Joules age. Find the age of each dog.
Joule: 5 years
Newton: Not born yet
Toby: 1 year
Joule: 9 years
Newton: 3 years
Toby: 8 year
Joule: 8 years
Newton: 4 years
Toby: 8 year
none of these
Joule: 12 years
Newton: 1 year
Toby: 5 year
Joule: 9 years
Newton: 3 years
Toby: 8 year
First, translate the problem into three equations. The statement, "Joule is three years older than twice Newton's age" is mathematically translated as
where 

The statement, "Newton is Toby's age younger than eleven years" is translated as
where 
The third statement, "Toby is one year younger than Joule" is

So these are our three equations. To figure out the age of these dogs, first I will plug the third equation into the second equation. We get
Plug this equation into the first equation to get
Solve for 

Divide both sides by 3
So Joules is 9 years old. Plug this value into the third equation to find Toby's age
Toby is 8 years old. Use this value to find Newton's age using the second equation
Now, we have the age of the following dogs:
Joule: 9 years
Newton: 3 years
Toby: 8 years
Example Question #1 : Solve Problems Leading To Two Linear Equations: Ccss.Math.Content.8.Ee.C.8c
Teachers at an elementary school have devised a system where a student's good behavior earns him or her tokens. Examples of such behavior include sitting quietly in a seat and completing an assignment on time. Jim sits quietly in his seat 2 times and completes assignments 3 times, earning himself 27 tokens. Jessica sits quietly in her seat 9 times and completes 6 assignments, earning herself 69 tokens. How many tokens is each of these two behaviors worth?
Sitting quietly and completing an assignment are each worth 4 tokens.
Sitting quietly is worth 3 tokens and completing an assignment is worth 7.
Sitting quietly is worth 7 tokens and completing an assignment is worth 3.
Sitting quietly is worth 9 tokens and completing an assignment is worth 3.
Sitting quietly is worth 3 tokens and completing an assignment is worth 9.
Sitting quietly is worth 3 tokens and completing an assignment is worth 7.
Since this is a long word problem, it might be easy to confuse the two behaviors and come up with the wrong answer. Let's avoid this problem by turning each behavior into a variable. If we call "sitting quietly" 


and

We can multiply the first equation by 

This allows us to cancel the 


A quick substitution tells us that 
Example Question #2 : Word Translations
Solve the following story problem:
Jack and Aaron go to the sporting goods store. Jack buys a glove for 







Let's call "
Let's call the amount of money Jack starts with "
Let's call the amount of money Aaron starts with "
We know Jack buys a glove for 



simplifying, 
We know Aaron buys 



The last important piece of information from the problem is Aaron starts with 
From before we know:
Plugging in:
so Aaron started with
Finally we plug 
Thus one jersey costs
Example Question #71 : New Sat Math Calculator
Read, but do not solve, the following problem:
Adult tickets to the zoo sell for $11; child tickets sell for $7. One day, 6,035 tickets were sold, resulting in $50,713 being raised. How many adult and child tickets were sold?
If 

6,035 total tickets were sold, and the total number of tickets is the sum of the adult and child tickets, 
Therefore, we can say 
The amount of money raised from adult tickets is $11 per ticket mutiplied by 


These two equations form our system of equations.
Example Question #501 : New Sat
Solve the following inequality for 
The first step is to square each side of the inequality.
Now simplify each side.
Now subtract the left side of the inequality to make it zero, so that we can use the quadratic formula.
Now we can use the quadratic formula.
Recall the quadratic formula.
Where 


In this case 


Now plug these values into the quadratic equation, and we get.
Now since we are dealing with an inequality, we put the least value on the left side, and the greatest value on the right. It will look like the following.
Certified Tutor
Certified Tutor
All PSAT Math Resources