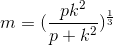All PSAT Math Resources
Example Questions
Example Question #1 : How To Find Out When An Equation Has No Solution
Consider the equation
Which of the following is true?
The equation has exactly one solution, which is negative.
The equation has no solution.
The equation has exactly two solutions, which are of unlike sign.
The equation has exactly one solution, which is positive.
The equation has exactly two solutions, which are of like sign.
The equation has exactly two solutions, which are of unlike sign.
Multiply the equation on both sides by LCM 
or
Substitution confirms that these are the solutions.
There are two solutions of unlike sign.
Example Question #3 : How To Find Out When An Equation Has No Solution
Which of the following equations has no solution?
Each of the equations in the other responses has no solution.
Each of the equations in the other responses has no solution.
The problem is basically asking for what value of 
has no solution.
We can simplify as folllows:
Since the absolute value of a number must be nonnegative, regardless of the value of 
Example Question #1 : Linear / Rational / Variable Equations
Consider the equation
Which of the following is true?
The equation has exacty one real solution, which is negative.
The equation has exacty one real solution, which is positive.
The equation has no real solutions.
The equation has exactly two real solutions, which are of like sign.
The equation has exactly two real solutions, which are of unlike sign.
The equation has exactly two real solutions, which are of unlike sign.
Multiply both sides by LCD 
or
There are two solutions of unlike sign.
Example Question #2 : Linear / Rational / Variable Equations
All of the following equations have no solution except for which one?
Since all of the equations have the same symbols save for one number, the problem is essentially as follows:
For what value of 
have a solution set other than the empty set?
We can simplify as follows:
If 



Therefore, the only equation among the given choices whose solution set is not the empty set is the equation
which is the correct choice.
Example Question #1 : How To Find Out When An Equation Has No Solution
Which of the following equations has no real solutions?
Each of the equations given in the other choices has at least one real solution.
We can examine each individually.
This equation has a solution.
This equation has a solution.
This equation has a solution.
This equation has no solution, since a fourth root of a number must be nonnegative.
The correct choice is ![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234982/gif.latex)
Example Question #1 : How To Find Out When An Equation Has No Solution
Solve 
No solutions
No solutions
By definition, the absolute value of an expression can never be less than 0. Therefore, there are no solutions to the above expression.
Example Question #1 : How To Find The Solution To A Rational Equation With Lcd
1
–1
–2
2
0
2
Example Question #2 : How To Find The Solution To A Rational Equation With Lcd
–bm/(m2 + 1)
–b/(m + 1)
bm/(m2 + 1)
b/(m2 + 1)
–b/(m2 – 1)
b/(m2 + 1)
Example Question #3 : How To Find The Solution To A Rational Equation With Lcd
In the equation below, 





Example Question #1 : How To Find The Solution To An Equation
If 6x = 42 and xk = 2, what is the value of k?
5
1/6
1/7
2/7
7
2/7
Solve the first equation for x by dividing both sides of the equation by 6; the result is 7. Solve the second equation for k by dividing both sides of the equation by x, which we now know is 7. The result is 2/7.
Certified Tutor
All PSAT Math Resources















































![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234933/gif.latex)
![-14 - \sqrt[3]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234934/gif.latex)
![14 - \sqrt[3]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234935/gif.latex)
![14 - \sqrt[4]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234936/gif.latex)
![14 - \sqrt[3]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234961/gif.latex)
![14 - \sqrt[3]{x - 7 } + 7 + \sqrt[3]{x - 7 } = -7 + 7 + \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234962/gif.latex)
![21 = \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234963/gif.latex)
![21^{3} =\left ( \sqrt[3]{x - 7 } \right )^{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234964/gif.latex)


![-14 - \sqrt[3]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234967/gif.latex)
![-14 - \sqrt[3]{x - 7 } - 7 + \sqrt[3]{x - 7 } = 7 - 7 + \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234968/gif.latex)
![-21 = \sqrt[3]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234969/gif.latex)
![\left (-21 \right )^{3} =\left ( \sqrt[3]{x - 7 } \right )^{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234970/gif.latex)


![14 - \sqrt[4]{x - 7 } = -7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234973/gif.latex)
![14 - \sqrt[4]{x - 7 } + 7 + \sqrt[4]{x - 7 } = -7 + 7 + \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234974/gif.latex)
![21 = \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234975/gif.latex)
![21^{4} =\left ( \sqrt[4]{x - 7 } \right )^{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234976/gif.latex)


![-14 - \sqrt[4]{x - 7 } = 7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234979/gif.latex)
![-14 - \sqrt[4]{x - 7 } - 7 + \sqrt[4]{x - 7 } = 7 - 7 + \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234980/gif.latex)
![-21 = \sqrt[4]{x - 7 }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/234981/gif.latex)