The graph has 3 waves between 0 and , meaning that the length of each of the waves is divided by 3, or .

The equation for this graph will be in the form where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

To write this equation, it is helpful to sketch a graph:

From sketching the maximum and the minimum, we can see that the graph is centered at and has an amplitude of 2.

The distance between the maximum and the minimum is half the wavelength. Here, it is . That means that the full wavelength is , so the frequency is 1.

The minimum occurs in the middle of the graph, so to figure out where it starts, subtract from the minimum's x-coordinate:

This graph's equation is

.

Our equation is in the form  

where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

We can look at the equation and see that the frequency, , is .

The period is , so in this case .

The equation for this function is in the form  

where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

By looking at the equation, we can see that the frequency, , is .

The period is , so in this case .

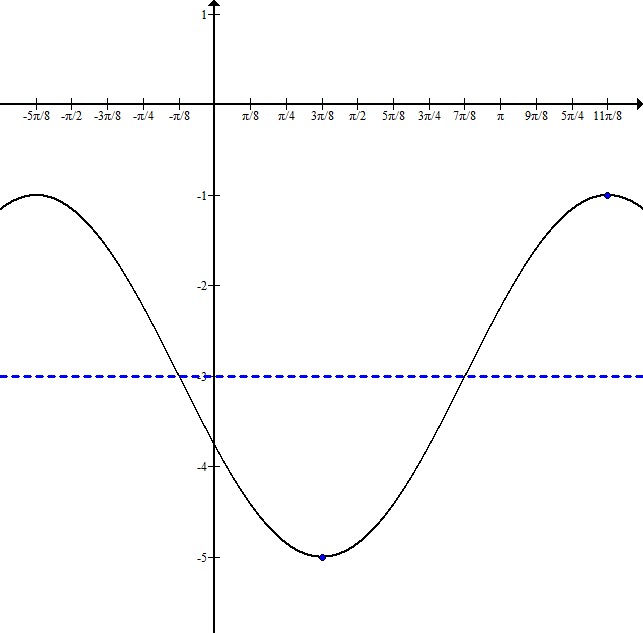
What could be the function for the following graph?

Begin by realizing we are dealing with a periodic function, so sine and cosine are your best bet. 

Next, note that the range of the function is and that the function goes through the point .

From this information, we can find the amplitude:

So our function must have a  out in front.

Also, from the point , we can deduce that the function has a vertical translation of positive two. 

The only remaining obstacle, is whether the function is sine or cosine. Recall that sine passes through , while cosine passes through . this means that our function must be a sine function, because in order to be a cosien graph, we would need a horizontal translation as well. 

Thus, our answer is:

For any equation in the form , the amplitude of the function is equal to .

In this case,  and , so our amplitude is .

The formula for the amplitude of a sine function is  from the form:

 .

In our function, .

Therefore, the amplitude for this function is .

Rewrite  so that it is in the form of:

The absolute value of  is the value of the amplitude.

For the sine function

 where 

the amplitude is given as  .

As such the amplitude for the given function

 is

.

The amplitude of a function is the amount by which the graph of the function travels above and below its midline. When graphing a sine function, the value of the amplitude is equivalent to the value of the coefficient of the sine. Similarly, the coefficient associated with the x-value is related to the function's period. The largest coefficient associated with the sine in the provided functions is 2; therefore the correct answer is .

The amplitude is dictated by the coefficient of the trigonometric function. In this case, all of the other functions have a coefficient of one or one-half.