and so the credited answer is .

We are given the hypotenuse and the side opposite of the angle in question. The trig function that relates these two sides is SIN. Therefore, we can write:

In order to solve for A, we need to take the inverse sin of both sides:

which becomes

Solve for theta by taking the inverse sine of both sides.

Since this angle is not valid for the given interval of theta, add  radians to this angle to get a valid answer in the interval.

First evaluate .

To evaluate inverse cosine, it is necessary to know the domain and range of inverse cosine. 

For: 

The domain  is only valid from .

 is only valid from .

The part is asking for the angle where the x-value of the coordinate is .  The only possibility on the unit circle is the second quadrant.  

Next, evaluate .

Using the same domain and range restrictions, the only valid angle for the given x-value is in the first quadrant on the unit circle.  

Therefore:

To find the correct value of , it is necessary to know the domain and range of inverse cosine.

Domain:  

Range:  

The question is asking for the specific angle when the x-coordinate is half.  

The only possibility is located in the first quadrant, and the point of the special angle is 

The special angle for this coordinate is .

In order to determine the value or values of , it is necessary to know the domain and range of the inverse sine function.

Domain:  

Range:  

The question is asking for the angle value of theta where the x-value is  under the range restriction.  Since  is located in the first and fourth quadrants, the range restriction makes theta only allowable from .  Therefore, the theta value must only be in the first quadrant.

The value of the angle when the x-value is  is  degrees.

The easiest way to solve this problem is to simplify the original expression. 

To find its inverse, let's exchange  and , 

Solving for 

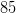
This can be written in the general form of:

. 

Since the maximum occurs at , we can arbitrarily choose  since cosine would be maximum when the inner term is equal to . 

To determine , let's determine the period first. 

The period is equal to twice the length between adjacent crest and trough.

For us that is:

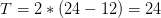
To determine , we do

To determine ,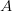 

To determine ,

The entire regression can therefore be written as:

The only thing that can be changed to keep the regression the same is the phase shift , and sign of the amplitude . The other two terms must be kept as they are. 

The y-intercept of a function is found by substituting . When we do this to each, we can determine the y-intercept. Don't forget your unit circle! 

Thus, the function with a y-intercept of  is . 

In the formula,

 .

 represents the phase shift.

Plugging in what we know gives us:

 .

Simplified, the phase is then .