The zeros of the function are the values of  where the function will be equal to zero.  In order to find these we set the numerator of the function equal to zero.

We only need to solve for  once,

So the zeros of this function are .

To solve for the points at which this function will be undefined, we set the denominator equal to zero and solve for .

And so the function is undefined at

This inequality wants all values where  is greater than .  So everything up until  is included and this is represented by having a dotted line on the graph or an open circle on a number line.

We will first begin by solving for the zeros and undefined points of the inequality.  We solve for the zeros by setting the numerator equal to zero.

And so the zeros of this function are at 

Now we will solve for the undefined points by setting the denominator equal to zero.  Since the denominator is , then whenever , the function is undefined.  Now we need to find for which values of  is each factor is greater than zero.

For , any value where  will be positive and we will be able to graph it.  For , any value where  will be positive.  Now, we can only graph these values up until  because the function is undefined here.  We are able to pick up the graph again once we reach .  The graph will look like the one below.

We begin by moving all of our terms to the left side of the inequality.

We then factor.

That means our left side will equal 0 when .  However, we also want to know the values when the left side is less than zero.  We can do this using test regions.  We begin by drawing a number line with our two numbers labeled.

We notice that our two numbers divide our line into three regions.  We simply need to try a test value in each region.  We begin with our leftmost region by selecting a number less than .  We then plug that value into the left side of our inequality to see if the result is positive or negative.  Any value (such as ) will give us a positive value.

We then repeat this process with the center region by selecting a value between our two numbers.  Any value (such as ) will result in a negative outcome.

Finally we complete the process with the rightmost region by selecting a value larger than .  Any value (such as ) will result in a positive value.

We then label our regions accordingly.

Since we want the result to be less than zero, we want the values between our two numbers.  However, since our left side can be less than or equal to zero, we can also include the two numbers themselves.  We can express this as

We begin by solving the equation for its zeros. This is done by changing the  sign into an  sign. 

Since we know the zeros of the equation, we can then check the areas around the zeros since we naturally have split up the real line into three sections :

First we check 

Therefore, the first interval can be included in our answer. Additionally, we know that  satisfies the equation, therefore we can say with certainty that the interval  is part of the answer. 

Next we check something in the second interval. Let , then

Therefore the second interval cannot be included in the answer.

Lastly, we check the third interval. Let , then

Which does satisfy the original equation. Therefore the third interval can also be included in the answer. Since we know that  satisfies the equation as well, we can include it in the interval as such: 

Therefore, 

Method 1:

1) Multiply-out the left side then rewrite the inequality as an equation:

2) Now rewrite as a quadratic equation and solve the equation:

3) Next set up intervals using the solutions and test the original inequality to   see where it holds true by using values for  on each interval.

4) The interval between  and  holds true for the original inequality.

5) Solution: 

Method 2:

Using a graphing calculator, find the graph.  The function is below the x-axis (less than ) for the x-values .  Using interval notation for , .

Method 3:

For the inequality , the variable expression in terms of is less than , and an inequality has a range of values that the solution is composed of.  This means that each of the solution values for  are strictly between the two solutions of .  'Between' is for a 'less than' case, 'Outside of' is for a 'greater than' case.

1) Write  as two simple inequalities:

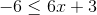
2) Solve the inequalities:

3) Write the final solution as a single compound inequality:

 For interval notation:

4) Now graph:

In order to solve this equation, we must first isolate the absolute value. In this case, we do it by dividing both sides by  which leaves us with:

When we work with absolute value equations, we're actually solving two equations. So, our next step is to set up these two equations: 

 and 

In both cases we solve for  by adding  to both sides, leaving us with

 and 

This can be rewritten as 

When we work with absolute value equations, we're actually solving two equations: 

 and 

Adding  to both sides leaves us with: 

 and 

Dividing by  in order to solve for  allows us to reach our solution:

 and 

Which can be rewritten as:

In order to solve for  we must first isolate the absolute value. In this case, we do it by dividing both sides by 2:

As with every absolute value problem, we set up our two equations:

 and 

We isolate  by adding  to both sides:

 and 

Finally, we divide by :

 and