All Precalculus Resources
Example Questions
Example Question #17 : Systems Of Equations
Solve the following system:
Our first step is to solve the bottom equation for 
so we can substitute it into the top equation:
Now we can plug in our y-values into the bottom equation to find our x-values:
Remember we cannot take a square root of a negative number without getting an imaginary number. As such, we'll just focus on the 
Our solution is then:
Example Question #18 : Systems Of Equations
Solve the following system for 
The first step is to solve the bottom equation for 


We now substitute this equation into the top equation:
we can now plug in our x-values into the bottom equation to find our y-values:




The solutions are then:
Example Question #19 : Systems Of Equations
Solve the following system:
We can solve this equation by using substitution since the bottom equation is already solved for 
We then solve the equation for our 
Finally, we substitute our values into the bottom equation to get our 



Our different solutions are then:
Example Question #1 : Solve Nonlinear Systems Of Equations
Solve the following system:
We can substitute the top equation into the bottom:

and solve for 
Now that we have our 



So, our values are
Example Question #1 : Solving Polynomial And Rational Inequalities
What is the solution to the following inequality?
First, we must solve for the roots of the cubic polynomial equation.
We obtain that the roots are 
Now there are four regions created by these numbers:
-
. In this region, the values of the polynomial are negative (i.e.plug in
and you obtain
-
. In this region, the values of the polynomial are positive (when
, polynomial evaluates to
)
-
. In this region the polynomial switches again to negative.
-
. In this region the values of the polynomial are positive
Hence the two regions we want are 

Example Question #2 : Solving Polynomial And Rational Inequalities
Solve the inequality.
First, subtract 

Then find the common denominator and simplify

Next, factor out the numerator

and set each of the three factor equal to zero and solve for 
The solutions are

Now plug in values between 
![\left(-1,\frac{1}{3}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462780/gif.latex)
![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462781/gif.latex)

Note that 

![\left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462782/gif.latex)
Thus, the solution to the inequality is
![(-\infty ,-1)\cup \left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462783/gif.latex)
Example Question #3 : Solving Polynomial And Rational Inequalities
Solve and graph:
1) Multiply both sides of the equation by the common denominator of the fractions:
2) Simplify:
3) For standard notation, and the fact that inequalities can be read backwards:
For interval notation:

4) Graph:

Example Question #4 : Solving Polynomial And Rational Inequalities
Solve and graph:
Graph the rational expression,
1) Because 


2) As 









3) As 








4) The funtion y is exists over the allowed x-intervals:
One approach for solving the inequality:
For
1) Determine where 


2) 


3) Then the solution is 
Another approach for solving the inequality:
1) Write 



2) 


3) Then the solution is 
Example Question #5 : Solving Polynomial And Rational Inequalities
Which of the following best describes the statement:
The undefined points of rational functions are vertical asymptotes.
The statement is always false
The statement is true in some cases and false in others
The statement is always true
The statement is always true
When solving for a point where the function will be undefined, you set the denominator equal to zero and solve for . This creates a vertical asymptote because when the denominator equals zero the function is undefined and we are solving for
. Say for example a function is undefined at
. So at all values of
where
this function is undefined creating a vertical asymptote.
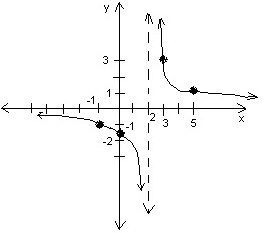
Example Question #1 : Solve And Graph Rational Inequalities




We begin by finding the zeros of the equation using the numerator.
So we know that the function will equal zero when 


And so the function is undefined at 
And if we graph these points we see something like below (which is our answer). Note that the dotted blue line is the vertical asymptote at 

Certified Tutor
All Precalculus Resources










































































![\left(-\infty ,\frac{1}{3}\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462779/gif.latex)


![\left(-1,\frac{1}{3}\right]\cup [2,\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462778/gif.latex)
![(-\infty ,-1)\cup \left[\frac{1}{3},2\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/462777/gif.latex)
















![[-\infty, 2] \cup [5, +\infty ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/294387/gif.latex)
![[2, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/477836/gif.latex)





























