All Precalculus Resources
Example Questions
Example Question #18 : Functions
Finding an inverse function.
Given
find



Finding an inverse function is essentially finding the output in terms of the input. To do this switch the independent and dependent variables. First set

Then
Now, to switch the role of the variables solve for x in terms of y.
or
So, y is now the independent variable, and x is the dependent variable. The final step is to write the inverse function in proper notation.
Set 

This gives

Example Question #11 : Relations And Functions
Which function below correctly translates 
The translation 







A vertical translation is up if 

Combining these, we get 
Example Question #21 : Functions
What is the domain of the following function?
-
The denominator becomes zero whenever cos(x) becomes -1 and this happens when x is an odd multiple of 
Example Question #1 : Graphing Functions
The angles are supplementary, therefore, the sum of the angles must equal 
Example Question #4 : Graphing Functions
Are 

Yes
No
Not enough information
Yes
Since supplementary angles must add up to 
Example Question #2 : Linear Functions
The angles containing the variable 
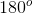
Because 
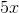
Example Question #1 : Graphs Of Polynomial Functions
For what values of 
None of the other answers
One can remember that if the multiplicity of a zero is odd then it passes through the x-axis and if it's even then it 'bounces' off the x-axis. You can think about this analytically as well. What happens when we plug a number into our function just slightly above or below a zero with an even multiplicity? You find that the sign is always positive. Whereas a zero with an odd multiplicity will yield a positive on one side and a negative on the other. For zeros with odd multiplicity this alters the sign of our output and the function passes through the x-axis. Whereas the zero with even multiplicity will output a number with the same sign just above and below its zero, thus it 'bounces' off the x-axis.
Example Question #2 : Graphs Of Polynomial Functions
For this particular question we are restricting the domain of both 

Let 

For what values of 

The cubic function will increase more quickly than the quadratic, so the quadratic function must have a head start. At 
The domain was restricted to nonnegative values, so this interval is our only answer.
Example Question #1 : Trigonometry

What is the 
Example Question #2 : Trigonometry

In the right triangle above, which of the following expressions gives the length of y?


Certified Tutor
Certified Tutor
All Precalculus Resources





















 .
.









 and
and  .
.

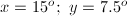


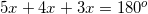














![[2,\infty]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/214527/gif.latex)















