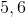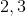We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Zeros Of A Polynomial

Factor the polynomial if the expression is equal to zero when $x=-6, -4,\ or\ 2$ .

x^3+8x^2+4x-48

Possible Answers:

(x+6)(x+4)(x-2)

(x-4)(x+2)(x-6)

(x-4)(x-2)(x+6)

(x+4)(x-2)(x-6)

Correct answer:

(x+6)(x+4)(x-2)

Explanation:

Knowing the zeroes makes it relatively easy to factor the polynomial.

The expression (x+6)(x+4)(x-2) fits the description of the zeroes.

Now we need to check the answer.

(x+4)(x-2)=x^2-2x+4x-8=x^2+2x-8

$\small (x^2+2x-8)(x+6)=x^3+6x^2+2x^2+12x-8x-48=x^3+8x^2+4x-48$

We are able to get back to the original expression, meaning that the answer is (x+6)(x+4)(x-2) .

Report an Error

Example Question #2 : Understanding Zeros Of A Polynomial

A polyomial with leading term $x^{3}$ has 6 as a triple root. What is this polynomial?

Possible Answers:

$x ^{3} -216$

$x ^{3} - 18 x^{2}+ 108x -216$

$x ^{3} +216$

$x ^{3} + 18 x^{2}+ 108x +216$

$x ^{3} + 18 x^{2}- 108x -216$

Correct answer:

$x ^{3} - 18 x^{2}+ 108x -216$

Explanation:

Since 6 is a triple root, and the degree of the polynomial is 3, the polynomial is $(x-6)^{3}$ , which we can expland using the cube of a binomial pattern.

$(x-6)^{3} =x ^{3} - 3\cdot x^{2} \cdot 6 + 3\cdot x\cdot 6 ^{2} -6^{3}$

$x ^{3} - 18 x^{2}+ 108x -216$

Report an Error

Example Question #91 : Pre Calculus

What is the highest multiplicity of the zeros in the polynomial f(x) =(x-3)^2(x+1)(x-2)

Possible Answers:

None of the other answers

Correct answer:

Explanation:

In the form given we can readily see that the polynomial has three zeros x = -1,2,3 . We observe that the zero at x = 3 has multiplicity of two whereas the others both have a multiplicity of one. This make our answer .

Report an Error

Example Question #92 : Pre Calculus

Find the zeros of the given polynomial. f(x) = (x+2)^2(x-1)(x+3)(x-5^3)

Possible Answers:

x = 1,-3

x = -5,-1,2,3

x= 1,-3,5

x = -3,-2,1,5

x = -2,5

Correct answer:

x = -3,-2,1,5

Explanation:

The zeros of the polynomial are the values of that set it equal to zero. In the given form we can clearly see that whenever any of the portions grouped in parentheses is equal to zero then the whole polynomial will be equal to zero. Since anything multiplied by zero is equal to zero. This fact lead us to our answer.

Report an Error

Example Question #15 : Polynomial Functions

Find the zeros of following polynomial:

x^5-x^3-5x^2+5

Possible Answers:

x=1,-1

$x=\sqrt[3]{5},1$

$x=-1,1,\sqrt[3]{5}$

x=1,5

$x=1,-1,\sqrt{5}$

Correct answer:

$x=-1,1,\sqrt[3]{5}$

Explanation:

To find the zeros we need to factor this polynomial. We start by grouping the terms and pulling out a common factor.

[x^5-x^3]+[-5x^2+5]=x^3(x^2-1)-5(x^2-1)

now our two groups have a common factor so we pull that out and we get

(x^2-1)(x^3-5)

this can be factored further into

(x-1)(x+1)(x^3-5)

and then we see that the x values that make each one of those terms 0 respectively are $1,-1,\sqrt[3]{5}$

Report an Error

Example Question #95 : Pre Calculus

Zeros of a cubic.

Find the zeros of the function

f(x)=x^3+3x^2-4x-12 .

Possible Answers:

$x=\{-3,-4\}$ .

$x=\{4,-4,-3\}$ .

$x=\{2,-3\}$ .

$x=\{2,-2,-3\}$ .

$x=\{3,-2,-3\}.$

Correct answer:

$x=\{2,-2,-3\}$ .

Explanation:

This is a 3rd order polynomial that can be factored. The leading coefficient is 1, so only the second term in each factor need be considered.

(3)(-4)=-12 , and $x\cdot x^2=x^3$ so f factors into

(x+3)(x^2-4) .

At this point the shortcut

(x^2-a^2)=(x+a)(x-a) can be used.

Now the final factorization is

(x+3)(x+2)(x-2) .

The zeros occur when each of the factors is zero, so

$x+3=0\Rightarrow x=-3$ ,

$x+2=0\Rightarrow x=-2$ , and

$x-2=0\Rightarrow x=2$ .

Report an Error

Example Question #93 : Pre Calculus

A polynomial with the leading term x^3 has 2 as a triple root. What is the polynomial?

Possible Answers:

x^3-6x^2+12x-8

x^3-8x^2+6x-12

x^3-12x^2+8x-6

x^3-2x^2+2x-2

x^3+6x^2-12x+8

Correct answer:

x^3-6x^2+12x-8

Explanation:

For a polynomial to have 2 as a triple root, 2 must be it's solution 3 times. Solving this backwards, we start by constucting the final equation and working backwards.

(x-2)(x-2)(x-2)=0

The above equation gives us 2 as a triple root, so the polynomial on the left is what we are looking for.

(x-2)(x-2)(x-2)

(x^2-4x+4)(x-2)

x^3-4x^2+4x-2x^2+8x-8

x^3-6x^2+12x-8

Report an Error

Example Question #97 : Pre Calculus

Zeros of a quadratic.

Find the roots of

y=12x^2+2x-4 .

Possible Answers:

$x=\{-\frac{2}{3},\frac{1}{2}\}$ .

$x=\{-\frac{2}{3}-,\frac{1}{2}\}$

$x=\{-\frac{2}{3},1\}$

$x=\{\frac{2}{3},\frac{1}{2}\}$

$x=\{-\frac{3}{2},\frac{1}{2}\}$ .

Correct answer:

$x=\{-\frac{2}{3},\frac{1}{2}\}$ .

Explanation:

Set y=0, then factor. The leading coefficient is 12, so its factors need to be considered. Trial and error will lead to 3 and 4 as the best choice combined with using 2 and -2 to give the last term.

Thus y=(3x+2)(4x-2) .

y=0 when either of the factors are 0.

So,

$3x+2=0\Rightarrow x=-\frac{3}{2}$ ,

and

$4x-2=0\Rightarrow x=\frac{1}{2}$ .

Report an Error

Example Question #94 : Pre Calculus

Find the zeros of the following polynomial:

x^2-5x+6

Possible Answers:

-2,-3

-5,-6

5,6

2,3

Correct answer:

2,3

Explanation:

To find the zeros of a polynomial, we have set it equal to 0, factor it, and solve for x.

x^2-5x+6=0

(x-2)(x-3)=0

$x-2=0\Rightarrow x=2$

$x-3=0\Rightarrow x=3$

Report an Error

Example Question #95 : Pre Calculus

Find the zeros of the following polynomials.

2x^2-3x-5

Possible Answers:

$\frac{-5}{2},1$

$\frac{5}{2}, -1$

3,5

-3,-5

Correct answer:

$\frac{5}{2}, -1$

Explanation:

To find the zeros, we must set the polynomial equal to 0, factor, and solve.

2x^2-3x-5=0

(2x-5)(x+1)=0

$x=\frac{5}{2},-1$

Report an Error

View Pre-Calculus Tutors

Yixuan
Certified Tutor

Macalester College, Bachelor in Arts, Mathematics and Statistics.

View Pre-Calculus Tutors

Njoku
Certified Tutor

Regents College Canterbury University, Bachelor in Arts, Political Science and Government. SUNY at Binghamton, Certificate, F...

View Pre-Calculus Tutors

Junzhe
Certified Tutor

Ohio State University-Main Campus, Bachelor of Science, Psychology.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Biology Tutors in Houston, Statistics Tutors in San Francisco-Bay Area, English Tutors in Atlanta, Math Tutors in Houston, Chemistry Tutors in Los Angeles, SSAT Tutors in Washington DC, SSAT Tutors in Phoenix, ISEE Tutors in Chicago, MCAT Tutors in Los Angeles, Chemistry Tutors in San Diego

Popular Courses & Classes

SSAT Courses & Classes in Atlanta, LSAT Courses & Classes in San Diego, Spanish Courses & Classes in Chicago, LSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Chicago, SSAT Test Prep in Denver, LSAT Test Prep in Houston, GMAT Test Prep in Miami, SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Diego, ISEE Test Prep in New York City, ISEE Test Prep in Seattle, GMAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Understanding Zeros Of A Polynomial

Example Question #2 : Understanding Zeros Of A Polynomial

Example Question #91 : Pre Calculus

Example Question #92 : Pre Calculus

Example Question #15 : Polynomial Functions

Example Question #95 : Pre Calculus

Example Question #93 : Pre Calculus

Example Question #97 : Pre Calculus

Example Question #94 : Pre Calculus

Example Question #95 : Pre Calculus

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: