We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Graphing Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : Find Roots Of Quadratic Equation Using Discriminant

Use the formula b² - 4ac to find the discriminant of the following equation: -3x² + 6x - 3 = 0.

Then state how many roots it has, and whether they are real or imaginary. Finally, use the quadratic function to find the exact roots of the equation.

Possible Answers:

Discriminant: 0

One real root: x = -1

Discriminant: 0

One real root: x = 1

Discriminant: 72

Two distinct real roots: $x=-1\pm \sqrt{2}$

Discriminant: 72

Two distinct real roots: $x=1\pm \sqrt{2}$

Discriminant: -72

Two distinct imaginary roots: $x=1\pm 2i$

Correct answer:

Discriminant: 0

One real root: x = 1

Explanation:

In the above equation, a = -3, b = 6, and c = -3. Therefore:

b² - 4ac = (6)² - 4(-3)(-3) = 36 - 36 = 0.

When the discriminant is greater than 0, there are two distinct real roots. When the discriminant is equal to 0, there is exactly one real root. When the discriminant is less than zero, there are no real roots, but there are exactly two distinct imaginary roots. In this case, there is exactly one real root.

Finally, we use the quadratic function to find these exact root. The quadratic formula is:

$x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$

Plugging in our values of a, b, and c, we get:

$x = \frac{-6\pm \sqrt{36 - 4\cdot -3\cdot -3}}{2\cdot -3}$

This simplifies to:

$x = \frac{-6\pm \sqrt{36 - 36}}{-6}$

which simplifies to

$x= \frac{-6\pm0}{-6}$

which gives us one answer: x = 1

This value of x is the one distinct real root of the given equation.

Report an Error

Example Question #3 : Find Roots Of Quadratic Equation Using Discriminant

Use the formula b² - 4ac to find the discriminant of the following equation: x² + 5x + 4 = 0.

Then state how many roots it has, and whether they are real or imaginary. Finally, use the quadratic function to find the exact roots of the equation.

Possible Answers:

Discriminant: 41

Two imaginary roots: $x=\frac{-5\pm 41i}{2}$

Discriminant: 0

One real root: $x=\frac{-5}{2}$

Discriminant: 9

Two real roots: x = -1 or x = -4

Discriminant: 9

Two real roots: x = 1 or x = 4

Discriminant: 41

Two imaginary roots: $x=\frac{5\pm 41i}{2}$

Correct answer:

Discriminant: 9

Two real roots: x = -1 or x = -4

Explanation:

In the above equation, a = 1, b = 5, and c = 4. Therefore:

b² - 4ac = (5)² - 4(1)(4) = 25 - 16 = 9.

Finally, we use the quadratic function to find these exact roots. The quadratic function is:

$x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$

Plugging in our values of a, b, and c, we get:

$x = \frac{-5\pm \sqrt{5^2 - 4\cdot 1\cdot 4}}{2\cdot 1}$

This simplifies to:

$x = \frac{-5\pm \sqrt{9}}{2}$

which simplifies to

$x=\frac{-5\pm3}{2}$

which gives us two answers:

x = -1 or x = -4

These values of x are the two distinct real roots of the given equation.

Report an Error

Example Question #4 : Find Roots Of Quadratic Equation Using Discriminant

Use the formula b² - 4ac to find the discriminant of the following equation: -x² + 3x - 3 = 0.

Then state how many roots it has, and whether they are real or imaginary. Finally, use the quadratic function to find the exact roots of the equation.

Possible Answers:

Discriminant: -21

Two imaginary roots: $x=\frac{-3\pm\sqrt{21}i}{2}$

Discriminant: -8

Two imaginary roots: $x=\frac{3\pm\sqrt{3}i}{2}$ .

Discriminant: 0

One real root: $x=\frac{3}{2}$

Discriminant: -8

Two imaginary roots: $x=\frac{-3\pm\sqrt{3}i}{2}$

Discriminant: -21

Two imaginary roots: $x=\frac{3\pm\sqrt{21}i}{2}$

Correct answer:

Discriminant: -8

Two imaginary roots: $x=\frac{3\pm\sqrt{3}i}{2}$ .

Explanation:

In the above equation, a = -1, b = 3, and c = -3. Therefore:

b² - 4ac = (3)² - 4(-1)(-3) = 9 - 12 = -3.

Finally, we use the quadratic function to find these exact roots. The quadratic function is:

$x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$

Plugging in our values of a, b, and c, we get:

$x = \frac{-3\pm \sqrt{3^2 - 4\cdot -1\cdot -3}}{2\cdot -1}$

This simplifies to:

$x = \frac{-3\pm \sqrt{-3}}{-2}$

Because $\sqrt{-3}=\sqrt{(-1)(3)}=\sqrt{3}i$ , this simplifies to $x=\frac{3\pm\sqrt{3}i}{2}$ . In other words, our two distinct imaginary roots are $x=\frac{3+\sqrt{3}i}{2}$ and $x=\frac{3-\sqrt{3}i}{2}$

Report an Error

Example Question #5 : Find Roots Of Quadratic Equation Using Discriminant

Use the formula b² - 4ac to find the discriminant of the following equation: x² + 2x + 10 = 0.

Then state how many roots it has, and whether they are real or imaginary. Finally, use the quadratic function to find the exact roots of the equation.

Possible Answers:

Discriminant: 36

Two real roots: x = 5 or x = -7

Discriminant: -36

Two imaginary roots: $-1\pm3i$

Discriminant: 0

One real root: x = -1

Discriminant: -36

Two imaginary roots: $1\pm3i$

Discriminant: 36

Two real roots: x = -5 or x = 7

Correct answer:

Discriminant: -36

Two imaginary roots: $-1\pm3i$

Explanation:

In the above equation, a = 1, b = 2, and c = 10. Therefore:

b² - 4ac = (2)² - 4(1)(10) = 4 - 40 = -36.

Finally, we use the quadratic function to find these exact roots. The quadratic function is:

$x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$

Plugging in our values of a, b, and c, we get:

$x = \frac{-2\pm \sqrt{2^2 - 4\cdot 1\cdot 10}}{2\cdot 1}$

This simplifies to:

$x = \frac{-2\pm \sqrt{-36}}{2}$

Because $\sqrt{-36}=\sqrt{(-1)(36)}=6i$ , this simplifies to $x=\frac{-2\pm6i}{2}$ . We can further simplify this to $-1\pm3i$ . In other words, our two distinct imaginary roots are -1+3i and -1-3i .

Report an Error

Example Question #6 : Find Roots Of Quadratic Equation Using Discriminant

Use the formula b² - 4ac to find the discriminant of the following equation: x² + 8x + 16 = 0.

Then state how many roots it has, and whether they are real or imaginary. Finally, use the quadratic function to find the exact roots of the equation.

Possible Answers:

Discriminant: 0

One real root: x = 0

Discriminant: 0

One real root: x = -4

Discriminant: 128

Two distinct real roots: $x=-4\pm4\sqrt{2}$

Discriminant: 0

One real root: x = 4

Discriminant: 72

Two distinct real roots: $x=4\pm4\sqrt2$

Correct answer:

Discriminant: 0

One real root: x = -4

Explanation:

In the above equation, a = 1, b = 8, and c = 16. Therefore:

b² - 4ac = (8)² - 4(1)(16) = 64 - 64 = 0.

Finally, we use the quadratic function to find these exact root. The quadratic formula is:

$x = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$

Plugging in our values of a, b, and c, we get:

$x = \frac{-8\pm \sqrt{8^2 - 4\cdot 1\cdot 16}}{2\cdot 1}$

This simplifies to:

$x = \frac{-8\pm \sqrt{0}}{2}$

which simplifies to

x=-4

This value of x is the one distinct real root of the given equation.

Report an Error

Example Question #1 : Amplitude, Period, Phase Shift Of A Trig Function

What is the amplitude of the following function?

$y = -24\sin(x-\pi)+14$

Possible Answers:

$\pi$

-24

-14

Correct answer:

Explanation:

When you think of a trigonometric function of the form y=Asin(Bx+C)+D, the amplitude is represented by A, or the coefficient in front of the sine function. While this number is -24, we always represent amplitude as a positive number, by taking the absolute value of it. Therefore, the amplitude of this function is 24.

Report an Error

Example Question #101 : Graphing Functions

Select the answer choice that correctly matches each function to its period.

Possible Answers:

$\sin x \rightarrow \pi$

$\cos x \rightarrow \pi$

$\tan x \rightarrow \pi$

$\cot x \rightarrow \pi$

$\sec x \rightarrow \pi$

$\csc x \rightarrow \pi$

$\sin x \rightarrow 2\pi$

$\cos x \rightarrow 2\pi$

$\tan x \rightarrow \pi$

$\cot x \rightarrow \pi$

$\sec x \rightarrow 2\pi$

$\csc x \rightarrow 2\pi$

$\sin x \rightarrow 2\pi$

$\cos x \rightarrow 2\pi$

$\tan x \rightarrow 2\pi$

$\cot x \rightarrow 2\pi$

$\sec x \rightarrow \pi$

$\csc x \rightarrow \pi$

$\sin x \rightarrow \pi$

$\cos x \rightarrow \pi$

$\tan x \rightarrow 2\pi$

$\cot x \rightarrow 2\pi$

$\sec x \rightarrow 2\pi$

$\csc x \rightarrow 2\pi$

$\sin x \rightarrow 2\pi$

$\cos x \rightarrow 2\pi$

$\tan x \rightarrow 2\pi$

$\cot x \rightarrow 2\pi$

$\sec x \rightarrow 2\pi$

$\csc x \rightarrow 2\pi$

Correct answer:

$\sin x \rightarrow 2\pi$

$\cos x \rightarrow 2\pi$

$\tan x \rightarrow \pi$

$\cot x \rightarrow \pi$

$\sec x \rightarrow 2\pi$

$\csc x \rightarrow 2\pi$

Explanation:

The following matches the correct period with its corresponding trig function:

$\sin x \rightarrow 2\pi$

$\cos x \rightarrow 2\pi$

$\tan x \rightarrow \pi$

$\cot x \rightarrow \pi$

$\sec x \rightarrow 2\pi$

$\csc x \rightarrow 2\pi$

In other words, sin x, cos x, sec x, and csc x all repeat themselves every $2\pi$ units. However, tan x and cot x repeat themselves more frequently, every $\pi$ units.

Report an Error

Example Question #2 : Amplitude, Period, Phase Shift Of A Trig Function

What is the period of this sine graph?

Trig period 1

Possible Answers:

$3\pi$

$\pi^2$

$\frac{3}{2}\pi$

$\frac{2}{3}\pi$

Correct answer:

$\frac{2}{3}\pi$

Explanation:

The graph has 3 waves between 0 and $2\pi$ , meaning that the length of each of the waves is $2\pi$ divided by 3, or $\frac{2}{3}\pi$ .

Report an Error

Example Question #3 : Amplitude, Period, Phase Shift Of A Trig Function

Write the equation for a cosine graph with a maximum at $\left( \frac{ \pi }{3} , 3 \right)$ and a minimum at $\left(\frac{ 4 \pi }{3} , -3 \right)$ .

Possible Answers:

$y = 2 \cos (x + \frac{ \pi }{3} )+ 1$

$y = 3 \cos (x - \frac{ \pi }{3} )$

$y = -3 \cos (x - \frac{ \pi } {3 })$

$y = 3 \cos (\frac{ 1}{2} ( x - \frac{ \pi }{3} ))$

$y = 2 \cos (\frac{ 1}{2} ( x + \frac{ \pi }{3} )) + 1$

Correct answer:

$y = 3 \cos (x - \frac{ \pi }{3} )$

Explanation:

In order to write this equation, it is helpful to sketch a graph:

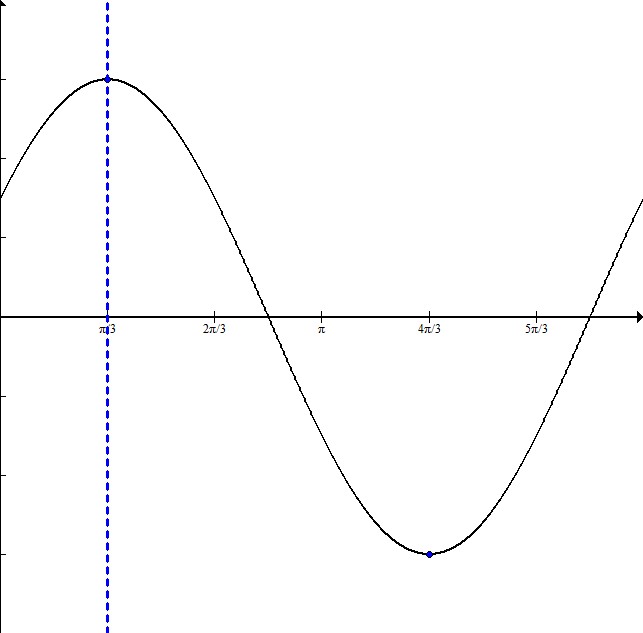
Trig graph 2

The dotted line is at $x = \frac{ \pi }{3}$ , where the maximum occurs and therefore where the graph starts. This means that the graph is shifted to the right $\frac{ \pi }{3}$ .

The distance from the maximum to the minimum is half the entire wavelength. Here it is $\frac{ 4 \pi }{3} - \frac{ \pi }{3} = \frac{ 3 \pi }{3} = \pi$ .

Since half the wavelength is $\pi$ , that means the full wavelength is $2 \pi$ so the frequency is just 1.

The amplitude is 3 because the graph goes symmetrically from -3 to 3.

The equation will be in the form $y = A \cdot \cos (f (x - h)) + k$ where A is the amplitude, f is the frequency, h is the horizontal shift, and k is the vertical shift.

This equation is

$y = 3 \cos (x - \frac{ \pi } {3 })$ .

Report an Error

Example Question #102 : Graphing Functions

Find the phase shift of F(t)=3sin(2t+4) .

Possible Answers:

-4

-2

Correct answer:

-2

Explanation:

In the formula,

F(t)=Asin(Bt-C)+D .

$\frac{C}{B}$ represents the phase shift.

Plugging in what we know gives us:

$\frac{C}{B}=\frac{-4}{2}$ .

Simplified, the phase is then .

Report an Error

View Pre-Calculus Tutors

Chernyeh
Certified Tutor

Purdue University-Main Campus, Bachelor of Science, Business Administration and Management.

View Pre-Calculus Tutors

Bhupinder
Certified Tutor

Panjab University, Bachelor of Engineering, Biotechnology. Hamburg University of Technology, Master of Science, Chemical Engi...

View Pre-Calculus Tutors

Nicole
Certified Tutor

College of St Benedict, Bachelor in Arts, Economics. University of South Florida-Main Campus, Master of Arts, Economics.

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Houston, GRE Tutors in Boston, Physics Tutors in San Francisco-Bay Area, English Tutors in Atlanta, Calculus Tutors in Washington DC, English Tutors in Seattle, Chemistry Tutors in Atlanta, ISEE Tutors in Miami, GMAT Tutors in Dallas Fort Worth, Chemistry Tutors in Dallas Fort Worth

Popular Courses & Classes

GRE Courses & Classes in Miami, LSAT Courses & Classes in Boston, ACT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in Phoenix, MCAT Courses & Classes in Phoenix, GRE Courses & Classes in Denver, SSAT Courses & Classes in Phoenix, GRE Courses & Classes in Houston, GMAT Courses & Classes in Boston, SSAT Courses & Classes in Denver

Popular Test Prep

GRE Test Prep in Houston, MCAT Test Prep in Miami, SSAT Test Prep in Boston, SAT Test Prep in Chicago, SAT Test Prep in New York City, GMAT Test Prep in Phoenix, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in Denver, LSAT Test Prep in Washington DC, GRE Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Graphing Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #4 : Find Roots Of Quadratic Equation Using Discriminant

Example Question #3 : Find Roots Of Quadratic Equation Using Discriminant

Example Question #4 : Find Roots Of Quadratic Equation Using Discriminant

Example Question #5 : Find Roots Of Quadratic Equation Using Discriminant

Example Question #6 : Find Roots Of Quadratic Equation Using Discriminant

Example Question #1 : Amplitude, Period, Phase Shift Of A Trig Function

Example Question #101 : Graphing Functions

Example Question #2 : Amplitude, Period, Phase Shift Of A Trig Function

Example Question #3 : Amplitude, Period, Phase Shift Of A Trig Function

Example Question #102 : Graphing Functions

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: