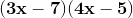To solve, factor and then solve for x.

In order to factor we need all our variables and constants on one side. Add 18 to both sides to make our function in a form for which we can factor.

Now we want to find factors of 18 that when added together give us 9. Thus we get the following factored form.

Now set each factor equal to zero and solve for x.

To find the zeros of the function, you need to factor the equation. Using trial and error, you should arrive at: . Then set those expressions equal to  so that your roots are .

To factor this polynomial it is prudent to recognize that there will only be two factors since the highest power is .

Then ask what numbers multiply to equal postive 35.

Next, what numbers can multiply to equal positive 12.

Let's try 7 and 5 for the last term and 3 and 4 for the first term.

Be sure to put an "x" in the first term of each factor.  

Choose the signs based on what the polynomial calls for. In our case we choose negative signs to get positive 35.

Foil these two factors and we get .

Which of the following could be the function modeled by this graph?

We can begin here by trying to identify a couple points  on the graph

We can see that it crosses the y-axis at 

Therefore, not only do we have a point, we have the y-intercept. This tells us that the equation of the line needs to have a  in it somewhere. Eliminate any option that do not have this feature.

Next, find the slope by counting up and over from the y-intercept to the next clear point.

It seems like the line goes up 5 and right 1 to the point 

This means we have a slope of 5, which means our equation must look like this:

For the linear function in point-slope form

The slope is equal to 

For this problem

we get

For the linear function in point-slope form

The slope is equal to 

For this problem

we get

By definition, the y-intercept is the point on the line that crosses the y-axis. This can be found by substituting  into the equation. When we do this with our equation, 

. 

Alternatively, you can remember  form, a general form for a line in which  is the slope and  is the y-intercept. 

Recall slope-intercept form, or . In this form,  is the slope and  is the y-intercept. Given our equation above, the slope must be the coefficient of the x, which is . 

The x-intercept of an equation is the point at which the line crosses the x-axis. Thus, we can find the x-intercept by plugging in . When we do this with our equation: 

Thus, our x-intercept is the point . 

First, we need to compute , the slope. We can do this with the slope formula

, sometimes called "rise over run"

 So we now have

Now in order to solve for  we substitute one of our points into the equation we found. It doesn't matter which point we use, so we'll use .

We then have:

Which becomes .

Hence we take our found value for  and plug it back into  to get

.