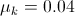Since the box is moving when the net force on the box is determined, we can calculate the coefficient of kinetic friction for the box. The first step is determining what the net force on the box would be in the absence of friction. The net force on the box is given by the equation .

The difference between the frictionless net force and the net force with friction is 0.8N. This means that the force of kinetic friction on the box is 0.8N, acting opposite the direction of motion. Knowing this, we can solve for the coefficient of kinetic friction using the equation 

Choice 2 is correct.  The formula for gravitational force, G, is , where k is a constant. The effect of doubling one mass and trebling the other is multiplicative, , so the answer is six-fold. The question attempts to confuse the respondent by forcing them to recall that the element of the equation which is squared is distance between objects.

You should be familiar with the following equation for the force of gravity.

To solve this problem, recognize that weight (F_g) is proportional to the inverse square of the radius. When the object was a distance of r (Earth’s radius) it had a weight of 500N. Now, the object is at a distance of 4r (radius of Earth plus the 3r distance that the object is moved to). With the proportion described above, we can see that the force is decreased by a factor of (4)².

The law of gravitation is written as , with G being equal to .

Since the radius of the two masses acting on each other is squared, and is found in the denominator, a decrease in the radius by a multiple of three will cause a nine-fold increase in the gravitational force.

Gravity is essentially a property of mass, and the force of gravitational attraction between two bodies is given by the formula:

In our scenario, the masses remain the same, and of course  is a constant, so the only thing that changes is the denominator.

On earth, .

The law of universal gravitation is equal to .

We can set these equations equal to one another and isolate  by dividing both sides by , the mass of an object on Earth.

Using the mass of the Earth, the radius of the Earth, and the gravitational constant, , we get a value of approximately if we solve for .

One way an object can be considered "weightless," is if it is accelerating downward at the same rate that it would be if it were free falling. This is why objects in an elevator whose cable had been cut would be "weightless." Therefore the answer is just for the block to be accelerating in the same magnitude and direction as the acceleration due to gravity, which is 

We know , and the force of gravity is:

Also, the equation for uniform circular motion, such as a satellite in orbit is:

Set  and substitute the acceleration due to circular motion into the equation. Solve for velocity.

This indicates that the only variables that affect the orbital speed are orbital radius and the mass of the Earth.

The block cannot provide any frictional force to the left because it is resting on a frictionless table. Whether the block is allowed to move or not, the tension force in the string is all generated by the suspended mass. The force in the string is equal and opposite to the gravitational force acting on the suspended mass.

The system is in equilibrium when no parts are in motion. Alternatively stated, the upward tension in the string is equal and opposite to the downwards force on the mass. If the block is not allowed to move as more mass is added, at some point the tensile force in the string will exceed its mechanical limits, and the string will break.

For the problem we need to understand Newton's second law: . The net upward forces and net downward forces must equal the product of mass and acceleration. Since the box is traveling upwards with an acceleration of 1m/s² we can indicate upward forces as positive and downward forces as negative. Indicating T as tension and Fg as the weight of the box, we can find the value of tension with the equation .