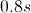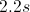The momentum formula is . We know that momentum is conserved during the collision, and that the final momentum must be eastward; thus, the initial net momentum must also be eastward, since momentum is a vector. Only one answer choice gives an eastward (positive) momentum.

Answer possibilities:

We can set this up as a conservation of momentum problem. The sum of the initial momentum for each object must equal the sum of the final momentum of each object.

We have two objects and four different velocities. The system must conserve momentum between the time before the collision and after the collision. We are given the mass of each object and their initial velocities.

We are given the magnitude of the billiard ball's final velocity, and told that it changes directions, thus becoming negative. Remember that both velocity and momentum are vector quantities.

Finally, we can solve of the final velocity of the bowling ball. We can predict that the bowling ball's velocity will be positive since the net initial velocity is positive, and the final billiard ball velocity is negative. The bowling ball must compensate for the negative momentum of the billiard ball.

The best way to solve this problem is to use the impulse, or change in momentum. Impulse can be calculate from either of two equations:

We can set these equations equal, and use the given values for mass and velocity to calculate the impulse.

We are given the applied force, allowing us to solve for the time.

Momentum is conserved in both elastic and inelastic collisions. During an elastic collision, kinetic energy is also conserved and the two objects remain separate after impact. During an inelastic collision, kinetic energy is lost to the surroundings and the objects traditionally stick together upon impact. The energy lost in an inelastic collision is generally transformed into heat or sound.

The only time momentum will not be conserved is when an outside force is introduced or the masses of objects do not remain constant.

This is a case of inelastic collision because the objects stay in contact after the impact. The total momentum in a system is always conserved, regardless of collision type. Here, the momentum before the collision is given by the sum of the individual momentum of each car, and the momentum after the collision is given by the singular momentum of the joined vehicles.

We are given the mass of each car and their initial velocities, allowing us to completely solve the left side of this equation.

We can now use the combined mass of both cars to solve for their final velocity.

Momentum is conserved in all situations. Here, we have an elastic collision, meaning that the objects do not stick together after the impact. Momentum is simply the product of mass and velocity, and it has the units .

We can solve this problem by setting the initial and final momentum of the system equal to each other. The momentum of the system will be the sum of the momentum of the parts.

The second ball contributes no momentum initially, because its initial velocity is zero. The total initial momentum comes from the initial velocity of the larger ball.

We know the mass of each ball and the final velocity of the smaller ball. Using these values, we can solve for the final velocity of the larger ball.

Momentum is given by the equation . Conservation of momentum states that .

The initial momentum is given by the sum of the initial momentums of the two objects. Because the second mass starts from rest, it becomes irrelevant in the equation.

After a perfectly inelastic collision, the two objects will stick together and their masses will add. The final velocity will apply to the combined mass of the two objects.

Since we know that , we can use our values from these calculations to solve for .

The mass of the second object must be 2kg.

A perfectly inelastic collision is when the two bodies stick together at the end. At the beginning the two balls are traveling separately with individual momentum values. Using the momentum equation , we can see that ball A has a momentum of (4kg)(7m/s) to the right and ball B has a momentum of (6kg)(8m/s) to the left. The final momentum would be the mass of both balls times the final velocity, (4+6)(v_f). We can solve for v_f through conservation of momentum; the sum of the initial momentum values must equal the final momentum.

Note: ball B's velocity is negative because they are traveling in opposite directions.

The negative sign indicates the direction in which the two balls are traveling. Since the sign is negative and we indicated that traveling to the left is negative, the two balls must be traveling 2m/s to the left after the perfectly inelastic collision.

Kinetic energy and potential energy are interconverted. While total energy is conserved, kinetic energy is allowed to increase or decrease, provided that potential energy does the opposite. For example, as the child in collision 1 is starting at the top of a ramp, she has potential energy, but no kinetic energy. At the bottom of the ramp, all the potential energy has been turned into kinetic energy.

Momentum, on the other hand, is conserved in every collision.

Momentum is always conserved in collisions, and is equal to the product of mass and velocity.