All MCAT Physical Resources
Example Questions
Example Question #13 : Translational Motion
Two children are playing on an icy lake. Child 1 weighs 50kg, and child 2 weighs 38kg. Child 1 has a backpack that weighs 10kg, and child 2 has a backpack that weighs 5kg.
Over the course of the afternoon, they collide many times. Four collisions are described below.
Collision 1:
Child 1 starts from the top of a ramp, and after going down, reaches the lake surface while going 
Collision 2:
Child 1 and child 2 are sliding in the same direction. Child 2, moving at 

Collision 3:
The two children collide while traveling in opposite directions at 
Collision 4:
The two children push off from one another’s back, and begin moving in exactly opposite directions. Child 2 moves with a velocity of 
In collision 4, what is the final velocity of child 1? Ignore friction and air resistance.
Cannot be determined from the information given
This is a reverse collision, and momentum is still conserved. The original momentum is zero.
Example Question #61 : Mcat Physical Sciences
Which of the following is a correct description of an inelastic collision?
Kinetic energy is conserved, but momentum is not
Momentum is conserved, but kinetic energy is not
Both kinetic energy and momentum are conserved
Kinetic energy is conserved, and momentum may be conserved
Neither kinetic energy nor momentum is conserved
Momentum is conserved, but kinetic energy is not
Momentum is conserved in any collision, but kinetic energy is only conserved in elastic collisions. So, an inelastic collision has conservation of momentum, but not conservation of kinetic energy.
Example Question #62 : Mcat Physical Sciences
In an elastic collision, which of the following quantities is not conserved?
Potential energy
All of these are conserved
Momentum
Mechanical energy
Kinetic energy
All of these are conserved
In an inelastic collision, kinetic energy is not conserved. In an elastic collision, kinetic energy is conserved and there is no transfer of energy to the surroundings.
Momentum is conserved regardless of the type of collision. All of the given quantities are conserved during an elastic collision.
Example Question #1 : Work
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 30o. The coefficient of kinetic friction for the ramp is 0.1.
What is the work done by gravity on the box?
Work is determined using the equation 




Notice how the work done by gravity is equal to the potential energy of the box at the top of the ramp. This is because mechanical energy is conserved in the system; thus, we can set the two equations equal to each other.
Example Question #2 : Work, Energy, And Power
What is the work done on a 


Work is represented by the product of force and displacement:
We are given the force on the box and the distance it travels. Use these values to calculate the work done.
Note that the mass of the box for this problem is irrelevant. There is no vertical displacement, so the force of gravity does not come into play. The only force that matters in this question is the "pushing force."
Example Question #1 : Work, Energy, And Power
Two students (student X and student Y) lift a boulder vertically from point A to point B. Student X directly lifts the boulder from point A to point B, whereas student Y uses a pulley to lift the boulder. This allows student Y to apply a force (

The vertical distance between point A and point B is 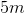
Student Z uses an inclined plane to lift the boulder and exerts only one third of 
the same because work is a state function in a gravitational field
different because work is a path function in a gravitational field
different because work is a state function in a gravitational field
the same because work is a path function in a gravitational field
the same because work is a state function in a gravitational field
Work is generally considered a path function. This means that the amount of work depends on the path taken.
Work in a gravitational field, however, is not a path function; it is a state function. This means that work is independent of the path taken in a gravitational field. This occurs because the force due to gravity acts only in one direction (downwards); therefore, the work performed with or against gravity will only depend on the vertical distance travelled.
In this question both students lift the boulder along the same vertical distance (a distance of 

Example Question #2 : Work, Energy, And Power
How much work is done to lift a 

The work done is equal to the gravitational potential energy of the block after it has been lifted.
The gravitational potential energy is calculated using the following formula:
We are given the mass and the change in height, and we know the acceleration due to gravity. Using these values, we can solve for the change in potential energy by multiplication.
Example Question #2 : Work, Energy, And Power
What is the work done by gravity if a 50kg block is pushed along a 40m track?
The work done by any force that is perpendicular to the displacement is equal to zero. Since the block is moving horizontally, the net force in the vertical direction will be equal to zero; therefore, work done by either gravity or the normal force will be equal to zero.
Example Question #3 : Work, Energy, And Power
An object of mass 100g moves in circular path of radius 0.5m, under the influence of a 15N force directed radially inwards towards the center of the path. How much work is done by this force as the object moves one quarter of the way around the circle?
4.8J
11.8J
47J
7.5J
0J
0J
Work is given by 

Example Question #1 : Work, Energy, And Power
A 2kg box slides down a ramp a distance of two meters before it reaches the ground. The ramp has an angle of 30o. The coefficient of kinetic friction for the ramp is 0.1.
What is the work done by the normal force on the box?
Remember that the work done by a force on an object is dependent on the angle of the force to the object's displacement. The normal force acts perpendicularly to the ramp, which means it has an angle of 90o with respect to the box's displacement.
Because 

Certified Tutor
Certified Tutor
All MCAT Physical Resources












































