All ISEE Upper Level Math Resources
Example Questions
Example Question #51 : Quadrilaterals
A kite has the area of 

The area of a kite is half the product of the diagonals, i.e.
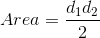
where 

Example Question #1 : Parallelograms

Give the area of the above parallelogram if 
Multiply height 

By the 30-60-90 Theorem:
and
The area is therefore
Example Question #1 : How To Find The Area Of A Parallelogram

Give the area of the above parallelogram if 
Multiply height 

By the 45-45-90 Theorem,

The area is therefore
Example Question #1 : How To Find The Area Of A Parallelogram
Three of the vertices of a parallelogram on the coordinate plane are 
Insufficient information is given to answer the problem.
As can be seen in the diagram, there are three possible locations of the fourth point of the parallelogram:

Regardless of the location of the fourth point, however, the triangle with the given three vertices comprises exactly half the parallelogram. Therefore, the parallelogram has double that of the triangle.
The area of the triangle can be computed by noting that the triangle is actually a part of a 12-by-12 square with three additional right triangles cut out:

The area of the 12 by 12 square is
The area of the green triangle is 
The area of the blue triangle is 
The area of the pink triangle is 
The area of the main triangle is therefore
The parallelogram has area twice this, or 
Example Question #1 : Parallelograms
One of the sides of a square on the coordinate plane has an endpoint at the point with coordinates 
The length of a segment with endpoints 




This is the length of one side of the square, so the area is the square of this, or 41.
Example Question #281 : Geometry

The area of the Parallelogram 


The height of the parallelogram is 


Also by the 45-45-90 Theorem,

The perimeter of the parallelogram is
Example Question #282 : Plane Geometry

Calculate the perimeter of the above parallelogram if 
By the 45-45-90 Theorem,
The perimeter of the parallelogram is
Example Question #7 : Parallelograms

Calculate the perimeter of the above parallelogram if 
By the 30-60-90 Theorem:

The perimeter of the parallelogram is
Example Question #8 : Parallelograms
Find the perimeter of a parallelogram with a base of 6in and a side of length 8in.
A parallelogram has 4 sides. A base (where the opposite side is equal) and a side (where the opposite side is equal). So, we will use the following formula:
where b is the base and s is the side of the parallelogram.
We know the base has a length of 6in. We also know the side has a length of 8in.
Knowing this, we can substitute into the formula. We get
Example Question #283 : Plane Geometry
Solve for 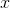

Find the sum of the interior angles of the polygon using the following equation where n is equal to the number of sides.
The sum of the angles must equal 360.
Certified Tutor
Certified Tutor
All ISEE Upper Level Math Resources