All ISEE Upper Level Math Resources
Example Questions
Example Question #284 : Plane Geometry
Two diagonals of a rhombus have lengths of 


The formula for the area of a rhombus is

where 

Example Question #285 : Plane Geometry
A rhombus has side length 

The area of a rhombus can be determined by the following formula:

where 

Example Question #1 : How To Find The Area Of A Rhombus
Find the area of a rhombus with one diagonal having a length of 12in and the other having a length two times the first diagonal.
To find the area of a rhombus, we will use the following formula:
where p and q are the lengths of the diagonals of the rhombus.
Now, we know one diagonal has a length of 12in. We also know the other diagonal is two times the first diagonal. Therefore, the second diagonal is 24in.
Knowing this, we can substitute into the formula. We get
Example Question #1 : Rhombuses
A rhombus has a perimeter of 
Like any polygon, the perimeter of the rhombus is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rhombus, all four sides have the same length, i.e.

where 
Example Question #2 : Rhombuses
A rhombus has the area of 

The area of a rhombus can be determined by the following formula:

where 

Example Question #1 : How To Find The Perimeter Of A Rhombus
One side of a rhombus measures 2 yards. Which of the following is equal to the perimeter?
All of the other choices give the correct perimeter.
A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 2 yards is 
Also,
The only choice that agrees with any of these measures is 288 inches, the correct choice.
Example Question #3 : Rhombuses
One side of a rhombus measures 

A rhombus has four sides of equal measure, so the perimeter of a rhombus with sidelength 

Example Question #4 : Rhombuses
Consider the rhombus below. Solve for 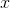

The total sum of the interior angles of a quadrilateral is 
Example Question #5 : Rhombuses

Note: Figure NOT drawn to scale.
The above depicts a rhombus and one of its diagonals. What is 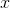
The diagonals of a rhombus bisect the angles.
The angle bisected must be supplementary to the 
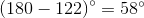

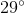
Example Question #1 : Rectangles
A rectangle on the coordinate plane has its vertices at the points 
What percent of the rectangle is located in Quadrant I?
The total area of the rectangle is
![\left [ 3- (-6) \right ] \times\left [ 4- (-2) \right ] = 9 \times 6 = 54](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/146123/gif.latex)
The area of the portion of the rectangle in Quadrant I is

Therefore, the portion of the rectangle in Quadrant I is

Certified Tutor
Certified Tutor
All ISEE Upper Level Math Resources


































































