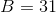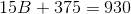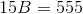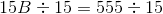Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Quadrilaterals

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Trapezoids

A trapezoid has height 20 inches. Its bases have sum 30 inches, and one base is 6 inches longer than the other. What is the area of this trapezoid?

Possible Answers:

$300 \textrm{ in}^{2}$

$600 \textrm{ in}^{2}$

$360 \textrm{ in}^{2}$

It cannot be determined from the information given.

$240 \textrm{ in}^{2}$

Correct answer:

$300 \textrm{ in}^{2}$

Explanation:

You do not need to find the individual bases; their sum, , is B + b . You can substitute B + b =30, h = 20 into the formula for the area of a trapezoid:

$A = \frac{1}{2} (B + b)h$

$A = \frac{1}{2}\cdot 30\cdot 20 = 300$ square inches.

Note that the fact that one base is inches longer is not important here.

Report an Error

Example Question #265 : Geometry

Trapezoidr

Find the area of the above trapezoid if $a=12\ cm$ , $b=14\ cm$ , and $h=10\ cm$ .

Figure not drawn to scale.

Possible Answers:

$130\ cm^2$

$100\ cm^2$

$110\ cm^2$

$90\ cm^2$

$120\ cm^2$

Correct answer:

$130\ cm^2$

Explanation:

The area of a trapezoid is given by

$Area=(\frac{b_{1}+b_{2}}{2})h$ ,

where $b_{}1$ , $b_{}2$ are the lengths of each base and is the altitude (height) of the trapezoid.

$b_{1}=a=12\ cm$

$b_{2}=b=14\ cm$

$h=10\ cm$

$Area=(\frac{b_{1}+b_{2}}{2})h=(\frac{12+14}{2})\times 10=13\times 10=130\ cm^2$

Report an Error

Example Question #2 : How To Find The Area Of A Trapezoid

A trapezoid has the base lengths of and . The area of the trapezoid is 8t^2 . Give the height of the trapezoid in terms of .

Possible Answers:

Correct answer:

Explanation:

The area of a trapezoid is given by

$Area=(\frac{b_{1}+b_{2}}{2})h$ ,

where $b_{}1$ , $b_{}2$ are the lengths of each base and is the altitude (height) of the trapezoid.

$Area=(\frac{b_{1}+b_{2}}{2})h=(\frac{3t+t}{2})\times h=8t^2\Rightarrow (2t)h=8t^2$

$\Rightarrow h=\frac{8t^2}{2t}=4t$

Report an Error

Example Question #3 : How To Find The Area Of A Trapezoid

In the following trapezoid b=2a and a=h . The area of the trapezoid is 54 square inches. Give the height of the trapezoid. Figure not drawn to scale.

Trap

Possible Answers:

$4\ in$

$5\ in$

$7\ in$

$3\ in$

$6\ in$

Correct answer:

$6\ in$

Explanation:

The area of a trapezoid is given by

$Area=(\frac{b_{1}+b_{2}}{2})h$ ,

where $b_{}1$ , $b_{}2$ are the lengths of each base and is the altitude (height) of the trapezoid.

$b_{1}=a$

$b_{2}=b=2a$

h=a

Substitute these values into the area formula:

$Area=(\frac{b_{1}+b_{2}}{2})h=(\frac{a+2a}{2})a=54\Rightarrow \frac{3a^2}{2}=54\Rightarrow a^2=36\Rightarrow a=6\ in$

Report an Error

Example Question #4 : How To Find The Area Of A Trapezoid

Square 3

What is the area of the shaded portion of the above square?

Possible Answers:

401

408

492

551

Correct answer:

492

Explanation:

Quadrilateral SQUR - the shaded region - is a trapezoid with bases $\overline{SR}$ and $\overline{QU }$ , and altitude $\overline{SQ}$ . The area of the trapezoid can be calculated using the formula

$A = \frac{1}{2} ( b_{1}+ b_{2} ) h$ ,

where $b_{1} = SR = 24$ and $b_{2} = QU$ , and h = SQ = 25 .

The length of $\overline{UA}$ can be found by setting c = 25 and b = 24 and applying the Pythagorean Theorem:

$a = \sqrt{c^{2} - b^{2}} = \sqrt{25^{2} - 24^{2}} =\sqrt{625- 576} = \sqrt{49} = 7$

Therefore,

QU = QA - UA = 24 - 7 = 17 .

Substituting:

$A = \frac{1}{2} ( b_{1}+ b_{2} ) h$

$A = \frac{1}{2} ( 24 + 17) 24$

$A = \frac{1}{2} \cdot 41 \cdot 24$

A = 492

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Trapezoid

Trapezoid

Note: Figure NOT drawn to scale.

The area of the above trapezoid is 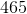465 . What is ?

Possible Answers:

B = 35

B = 42

B = 37

B = 31

B = 47

Correct answer:

B = 37

Explanation:

Substitute A = 465, b = 25, h = 15 into the formula for the area of a trapezoid:

$\frac{1}{2} (B + b)h = A$

$\frac{1}{2} (B + 25) \cdot 15 = 465$

$2 \cdot \frac{1}{2} (B + 25) \cdot 15 = 2 \cdot 465$

$(B + 25) \cdot 15 = 930$

15 B + 375 = 930

15 B + 375 - 375 = 930 - 375

15 B = 555

$15 B \div 15 = 555\div 15$

B = 37

Report an Error

Example Question #41 : Quadrilaterals

Cassie is making a kite for her little brother. She has two plastic tubes to use as the skeleton, measuring inches and inches. If these two tubes represent the diagnals of the kite, how many square inches of paper will she need to make the kite?

Possible Answers:

Correct answer:

Explanation:

To find the area of a kite, use the formula $\frac{1}{2}ab$ , where represents one diagnal and represents the other.

Since Cassie has one tube measuring inches, we can substitute for . We can also substitute the other tube that measures inches in for .

$\frac{1}{2}(7)(12)=42\ in^{2}$

Report an Error

Example Question #2 : How To Find The Area Of A Kite

Two diagonals of a kite have the lengths of $10\ in$ and $6\ in$ . Give the area of the kite.

Possible Answers:

$45\ in^2$

$60\ in^2$

$36\ in^2$

$30\ in^2$

$80\ in^2$

Correct answer:

$30\ in^2$

Explanation:

The area of a kite is half the product of the diagonals, i.e.

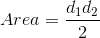
$Area=\frac{d_{1}d_{2}}{2}$ ,

where $d_{1}$ and $d_{2}$ are the lengths of the diagonals.

$Area=\frac{d_{1}d_{2}}{2}=\frac{6\times 10}{2}=30\ in^2$

Report an Error

Example Question #272 : Geometry

In the following kite, $a=10\ cm$ , $b=15\ cm$ and $\angle C=120^{\circ}$ . Give the area of the kite. Figure not drawn to scale.

Kite

Possible Answers:

$150\sqrt{3}\ cm^2$

$150\ cm^2$

$75\sqrt{3}\ cm^2$

$75\sqrt{2}\ cm^2$

$75\ cm^2$

Correct answer:

$75\sqrt{3}\ cm^2$

Explanation:

When you know the length of two unequal sides of a kite and their included angle, the following formula can be used to find the area of a kite:

$Area=ab\times sinC$ ,

where are the lengths of two unequal sides, is the angle between them and sin is the sine function.

$Area=ab\times sinC=10\times 15\times sin120^{\circ}=10\times 15\times \frac{\sqrt{3}}{2}\Rightarrow Area=75\sqrt{3}\ cm^2$

Report an Error

Example Question #3 : How To Find The Area Of A Kite

Find the area of a kite with one diagonal having length 18in and the other diagonal having a length that is half the first diagonal.

Possible Answers:

$76\text{in}^2$

$81\text{in}^2$

$162\text{in}^2$

$54\text{in}^2$

$108\text{in}^2$

Correct answer:

$81\text{in}^2$

Explanation:

To find the area of a kite, we will use the following formula:

$A = \frac{pq}{2}$

where p and q are the lengths of the diagonals of the kite.

Now, we know the length of one diagonal is 18in. We also know the other diagonal is half of the first diagonal. Therefore, the second diagonal has a length of 9in.

Knowing this, we can substitute into the formula. We get

$A = \frac{18\text{in} \cdot 9\text{in}}{2}$

$A = \frac{162\text{in}^2}{2}$

$A = 81\text{in}^2$

Report an Error

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Mike Bahaa
Certified Tutor

Concordia University-Ann Arbor, Master of Arts Teaching, Mathematics Teacher Education.

View Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Miami, Spanish Tutors in San Diego, Computer Science Tutors in Los Angeles, Calculus Tutors in Houston, Physics Tutors in San Francisco-Bay Area, Math Tutors in Los Angeles, Chemistry Tutors in Miami, ACT Tutors in Seattle, French Tutors in San Francisco-Bay Area, ACT Tutors in Dallas Fort Worth

Popular Courses & Classes

SSAT Courses & Classes in Washington DC, ISEE Courses & Classes in Seattle, LSAT Courses & Classes in Atlanta, Spanish Courses & Classes in New York City, SAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, GRE Courses & Classes in Atlanta, ACT Courses & Classes in Los Angeles, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Phoenix

Popular Test Prep

ACT Test Prep in Los Angeles, SAT Test Prep in Chicago, SSAT Test Prep in Atlanta, SSAT Test Prep in Houston, GMAT Test Prep in Denver, MCAT Test Prep in Seattle, SAT Test Prep in San Diego, LSAT Test Prep in Phoenix, GRE Test Prep in Miami, SSAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Quadrilaterals

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #2 : Trapezoids

Example Question #265 : Geometry

Example Question #2 : How To Find The Area Of A Trapezoid

Example Question #3 : How To Find The Area Of A Trapezoid

Example Question #4 : How To Find The Area Of A Trapezoid

Example Question #1 : How To Find The Length Of The Side Of A Trapezoid

Example Question #41 : Quadrilaterals

Example Question #2 : How To Find The Area Of A Kite

Example Question #272 : Geometry

Example Question #3 : How To Find The Area Of A Kite

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: