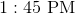Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Upper Level Math : Circles

Study concepts, example questions & explanations for ISEE Upper Level Math

Create An Account

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

Example Question #1 : How To Find The Area Of A Sector

While visiting a history museum, you see a radar display which consists of a circular screen with a highlighted wedge with an angle of $65^{\circ}$ . If the screen has a radius of 4 inches, what is the area of the highlighted wedge?

Possible Answers:

2.89 in^2

$9.08\pi in^2$

$14.23\pi in^2$

$2.89\pi in^2$

Correct answer:

$2.89\pi in^2$

Explanation:

To begin, let's recall our formula for area of a sector.

$A_{sector}=\frac{\theta}{360^{\circ}}\pi r^2$

Now, we have theta and r, so we just need to plug them in and simplify!

$A_{sector}=\frac{65^{\circ}}{360^{\circ}}\pi (4in)^2=2.89\pi in^2$

So our answer is $2.89\pi in^2$

Report an Error

Example Question #1 : Sectors

A giant clock has a minute hand six feet long. How far, in inches, did the tip move between noon and 1:20 PM?

Possible Answers:

$768 \pi \textrm{ in}$

$48 \pi \textrm{ in}$

$96\pi \textrm{ in}$

$384 \pi \textrm{ in}$

$192 \pi \textrm{ in}$

Correct answer:

$192 \pi \textrm{ in}$

Explanation:

The distance that the tip of the minute hand moves during one hour is the circumference of a circle with radius 6 feet. This circumference is $2\pi r = 2 \pi \times 6 = 12\pi$ feet. One hour and twenty minutes is $1 \frac{1}{3}$ hours, so the tip of the hand moved $1 \frac{1}{3} \times 12 \pi = 16 \pi$ feet, or $16 \pi \times 12 = 192 \pi$ inches.

Report an Error

Example Question #2 : Sectors

A giant clock has a minute hand three feet long. How far, in inches, did the tip move between noon and 12:20 PM?

Possible Answers:

$36\pi \textrm{ in}$

$12\pi \textrm{ in}$

It is impossible to tell from the information given

$24\pi \textrm{ in}$

$18\pi \textrm{ in}$

Correct answer:

$24\pi \textrm{ in}$

Explanation:

The distance that the tip of the minute hand moves during one hour is the circumference of a circle with radius feet. This circumference is $2\pi r = 2 \pi \times 3 = 6\pi$ feet. minutes is one-third of an hour, so the tip of the minute hand moves $\frac{1}{3} \times 6\pi = 2\pi$ feet, or $2\pi \times 12 = 24\pi$ inches.

Report an Error

Example Question #3 : Sectors

Inscribed

In the above figure, express in terms of .

Possible Answers:

$y = \frac{1}{2}x - 10$

$y = x- \frac{27}{4}$

$y = x- \frac{1}{4}$

$y = \frac{1}{2}x - \frac{3}{2}$

Correct answer:

$y = x- \frac{27}{4}$

Explanation:

The measure of an arc - $\overarc{AB}$ - intercepted by an inscribed angle - $\angle ACB$ - is twice the measure of that angle, so

$m \overarc{AB} = 2 \cdot m \angle ACB$

4y + 13 = 2 (2x- 7)

4y + 13 = 4x- 14

4y + 13 - 13 = 4x- 14 - 13

4y = 4x- 27

$\frac{4y}{4} = \frac{4x- 27}{4}$

$y = x- \frac{27}{4}$

Report an Error

Example Question #4 : Sectors

Intercepted

In the above diagram, radius OA = 12 .

Give the length of $\overarc {AB}$ .

Possible Answers:

$\frac{288\pi }{5}$

$\frac{24 \pi }{5}$

$\frac{72 \pi }{5}$

$\frac{48 \pi }{5}$

Correct answer:

$\frac{48 \pi }{5}$

Explanation:

The circumference of a circle is $2 \pi$ multiplied by its radius , so

$C = 2 \pi \cdot OA = 2 \pi \cdot 12 = 24 \pi$ .

$\angle ACB$ , being an inscribed angle of the circle, intercepts an arc $\overarc {AB}$ with twice its measure:

$m \overarc {AB} = 2 \cdot m\angle ACB = 2 \cdot 72 ^{\circ } = 144 ^{\circ }$

The length of $\overarc {AB}$ is the circumference multiplied by $\frac{144}{360}$ :

$\frac{144}{360} \times 24 \pi = \frac{48 \pi }{5}$ .

Report an Error

Example Question #5 : Sectors

Possible Answers:

1.44in

$4.54\pi in$

4.54in

$3.01\pi in$

Correct answer:

4.54in

Explanation:

To begin, let's recall our formula for length of an arc.

$Arc=\frac{\theta}{360^{\circ}}2 \pi r$

Now, just plug in and simplify

$Arc=\frac{65^{\circ}}{360^{\circ}}2 \pi (4in)=\frac{13^{\circ}}{9^{\circ}}\pi in\approx 4.54in$

So, our answer is 4.54in

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

A giant clock has a minute hand four feet long. Since noon, the tip of the minute hand has traveled $10 \pi$ feet. What time is it now?

Possible Answers:

$1:30 \textrm{ PM}$

$1:15 \textrm{ PM}$

$1:45 \textrm{ PM}$

$12:45 \textrm{ PM}$

$1:20 \textrm{ PM}$

Correct answer:

$1:15 \textrm{ PM}$

Explanation:

The circumference of the path traveled by the tip of the minute hand over the course of one hour is:

$C = 2 \pi r = 2 \pi \cdot 4 = 8 \pi$ feet.

Since the tip of the minute hand has traveled $10 \pi$ feet since noon, the minute hand has made

$\frac{10 \pi }{8 \pi } = \frac{5}{4} = 1 \frac{1}{4}$ revolutions. Therefore, $1 \frac{1}{4}$ hours have elapsed since noon, making the time 1:15 PM.

Report an Error

Example Question #2 : How To Find The Angle Of A Sector

Inscribed angle

Figure NOT drawn to scale

Refer to the above diagram. $\overarc {ABC}$ is a semicircle. Evaluate $m \overarc {BCA}$ given $\measuredangle B=90^\circ$ .

Possible Answers:

$302^{\circ }$

$292^{\circ }$

$312^{\circ }$

$282^{\circ }$

Correct answer:

$312^{\circ }$

Explanation:

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, $\angle B$ , which intercepts the semicircle $\overarc {ABC}$ , is such an angle. Consequently, $\bigtriangleup ABC$ is a right triangle, and $\angle A$ and $\angle C$ are complementary angles. Therefore,

$m \angle A + m \angle C = 90 ^{\circ }$

$y + \left ( \frac{y}{3}+2\right ) = 90$

$y + \frac{1}{3}y +2 = 90$

$\frac{4}{3}y +2 = 90$

$\frac{4}{3}y +2 - 2 = 90 - 2$

$\frac{4}{3}y = 88$

$\frac{3}{4} \cdot \frac{4}{3}y = \frac{3}{4} \cdot 88$

y = 66

$m \angle C = \left (\frac{y}{3}+ 2 \right ) ^{\circ }=\left ( \frac{66}{3}+ 2 \right )^{\circ }=( 22 + 2 )^{\circ }= 24^{\circ }$

Inscribed $\angle C$ intercepts an arc with twice its angle measure; this arc is $\overarc {AB}$ , so

$m \overarc {AB} = 2 \cdot m \angle C = 2 \cdot 24 ^{\circ } = 48 ^{\circ }$ .

The major arc corresponding to this minor arc, $\overarc {BCA}$ , has measure

$m \overarc {BCA} = 360 ^{\circ } - m \overarc {AB} = 360 ^{\circ } - 48^{\circ } = 312^{\circ }$

Report an Error

Example Question #221 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Inscribed angle

Note: Figure NOT drawn to scale

Refer to the above diagram. $\overarc {ABC}$ is a semicircle. Evaluate $m \overarc {AB}$ .

Possible Answers:

$79 ^{\circ }$

$69^{\circ }$

$64 ^{\circ }$

$74 ^{\circ }$

Correct answer:

$74 ^{\circ }$

Explanation:

An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, $\angle B$ , which intercepts the semicircle $\overarc{ABC}$ , is such an angle. Consequently,

$m \angle B = 90 ^{\circ }$

4x-18 = 90

4x - 18 + 18 = 90 + 18

4x = 108

$4x \div 4 = 108 \div 4$

x = 27

$m \angle C = (x+10)^{\circ } = (27+10)^{\circ }= 37^{\circ }$

Inscribed $\angle C$ intercepts an arc with twice its angle measure; this arc is $\overarc{AB}$ , so

$m \widehat{AB} = 2 \cdot m \angle C = 2 \cdot 37 ^{\circ } = 74 ^{\circ }$ .

Report an Error

Example Question #4 : How To Find The Angle Of A Sector

Intercepted

In the above diagram, radius AO = 20 .

Calculate the length of $\overarc {AB}$ .

Possible Answers:

$32 \pi$

$40 \pi$

$8 \pi$

$16 \pi$

Correct answer:

$16 \pi$

Explanation:

Inscribed $\angle ACB$ , which measures $72 ^{\circ }$ , intercepts an arc with twice its measure. That arc is $\overarc {AB}$ , which consequently has measure

$72 ^{\circ } \times 2 = 144 ^{\circ }$ .

This makes $\overarc {AB}$ an arc which comprises

$\frac{144}{360} = \frac{144 \div 72}{360 \div 72} = \frac{2}{5}$

of the circle.

The circumference of a circle is $2 \pi$ multiplied by its radius, so

$C = 2 \pi r = 2\pi \cdot 20 = 40 \pi$ .

The length of $\overarc {AB}$ is $\frac{2}{5}$ of this, or $\frac{2}{5} \cdot 40 \pi = 16 \pi$ .

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 Next →

View Tutors

Reuben
Certified Tutor

University of Alberta, Bachelor of Science, Mathematics.

View Tutors

Pushpendra
Certified Tutor

university of allahabad, Bachelor of Science, Mathematics.

View Tutors

Jaroslaw
Certified Tutor

Heriot Watt University, Master of Science, Physics. Heriot Watt University, Doctor of Science, Theoretical and Mathematical P...

All ISEE Upper Level Math Resources

6 Diagnostic Tests 244 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Dallas Fort Worth, LSAT Tutors in Seattle, Math Tutors in Phoenix, SSAT Tutors in Los Angeles, Computer Science Tutors in Philadelphia, English Tutors in San Diego, GMAT Tutors in Phoenix, LSAT Tutors in Denver, Spanish Tutors in Phoenix, ISEE Tutors in San Francisco-Bay Area

Popular Courses & Classes

GMAT Courses & Classes in Washington DC, Spanish Courses & Classes in Los Angeles, LSAT Courses & Classes in Chicago, ISEE Courses & Classes in Miami, ISEE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Washington DC, GRE Courses & Classes in Denver, SSAT Courses & Classes in Boston, ACT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Seattle, GRE Test Prep in New York City, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Chicago, LSAT Test Prep in Phoenix, ACT Test Prep in Boston, SSAT Test Prep in Houston, GRE Test Prep in Houston, GMAT Test Prep in Houston, LSAT Test Prep in San Francisco-Bay Area

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Upper Level Math : Circles

Study concepts, example questions & explanations for ISEE Upper Level Math

All ISEE Upper Level Math Resources

Example Questions

Example Question #1 : How To Find The Area Of A Sector

Example Question #1 : Sectors

Example Question #2 : Sectors

Example Question #3 : Sectors

Example Question #4 : Sectors

Example Question #5 : Sectors

Example Question #1 : How To Find The Angle Of A Sector

Example Question #2 : How To Find The Angle Of A Sector

Example Question #221 : Isee Upper Level (Grades 9 12) Mathematics Achievement

Example Question #4 : How To Find The Angle Of A Sector

All ISEE Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: