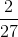We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : ISEE Lower Level (grades 5-6) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #292 : How To Multiply Fractions

Solve:

$\small \frac{4}{8}\times\frac{3}{4}$

Possible Answers:

$\small \frac{1}{2}$

$\small \frac{2}{3}$

$\small \frac{1}{4}$

$\small \frac{7}{9}$

$\small \frac{3}{8}$

Correct answer:

$\small \frac{3}{8}$

Explanation:

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator.

$\small \small \frac{4}{8}\times\frac{3}{4}=\frac{12}{32}$

$\small \frac{12}{32}$ can be reduced by dividing both sides by $\small 4$

$\small \frac{12}{32}\div\frac{4}{4}=\frac{3}{8}$

Report an Error

Example Question #293 : How To Multiply Fractions

Solve:

$\small \frac{7}{8}\times\frac{1}{3}$

Possible Answers:

$\small \frac{5}{27}$

$\small \frac{7}{21}$

$\small \frac{7}{24}$

$\small \frac{9}{11}$

$\small \frac{4}{5}$

Correct answer:

$\small \frac{7}{24}$

Explanation:

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator.

$\small \small \frac{7}{8}\times\frac{1}{3}=\frac{7}{24}$

Report an Error

Example Question #294 : How To Multiply Fractions

Solve:

$\small \frac{1}{5}\times\frac{1}{8}$

Possible Answers:

$\small \frac{5}{6}$

$\small \frac{1}{40}$

$\small \frac{2}{40}$

$\small \frac{1}{20}$

$\small \frac{1}{12}$

Correct answer:

$\small \frac{1}{40}$

Explanation:

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator.

$\small \small \frac{1}{5}\times\frac{1}{8}=\frac{1}{40}$

Report an Error

Example Question #2941 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

Solve the following:

$\small \frac{1}{3}\times\frac{1}{9}$

Possible Answers:

$\small \frac{2}{27}$

$\small \frac{1}{6}$

$\small \frac{5}{27}$

$\small \frac{1}{28}$

$\small \frac{1}{27}$

Correct answer:

$\small \frac{1}{27}$

Explanation:

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator.

$\small \small \frac{1}{3}\times\frac{1}{9}=\frac{1}{27}$

Report an Error

Example Question #543 : Fractions

Solve:

$\small \frac{2}{5}\times\frac{1}{7}$

Possible Answers:

$\small \frac{1}{15}$

$\small \frac{1}{5}$

$\small \frac{2}{35}$

$\small \frac{2}{7}$

$\small \frac{7}{8}$

Correct answer:

$\small \frac{2}{35}$

Explanation:

When we multiply fractions, we multiply the numerator by the numerator and the denominator by the denominator.

$\small \small \frac{2}{5}\times\frac{1}{7}=\frac{2}{35}$

Report an Error

Example Question #1901 : Numbers And Operations

Jessica made gallons of punch. $\frac{1}{5}$ of the punch was water. How many gallons of water did she use to make the punch?

Possible Answers:

$\frac{3}{5}$

$\frac{4}{5}$

$\frac{2}{5}$

Correct answer:

$\frac{2}{5}$

Explanation:

A keyword in our question that gives us a clue that we are going to multiply to solve this problem is the word "of". $\frac{1}{5}$ of the punch is water.

We know that we have gallons of punch so we can set up our multiplication problem.

$\frac{1}{5}\times2$

2 5

$\frac{1}{5}\times2$ which means $\frac{1}{5}$ of each group of $2=\frac{2}{5}$

Report an Error

Example Question #1 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Ronda made gallons of punch. $\frac{1}{5}$ of the punch was water. How much water did she use to make the punch?

Possible Answers:

$\frac{2}{5}$

$\frac{1}{5}$

$\frac{3}{5}$

Correct answer:

$\frac{3}{5}$

Explanation:

A keyword in our question that gives us a clue that we are going to multiply to solve this problem is the word "of". $\frac{1}{5}$ of the punch is water.

We know that we have gallons of punch so we can set up our multiplication problem.

$\frac{1}{5}\times3$

3 5

$\frac{1}{5}\times3$ which means $\frac{1}{5}$ of each group of $3=\frac{3}{5}$

Report an Error

Example Question #2 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Mary-Beth made gallons of punch. $\frac{1}{5}$ of the punch was water. How much water did she use to make the punch?

Possible Answers:

$\frac{3}{5}$

$\frac{2}{5}$

$\frac{4}{5}$

Correct answer:

$\frac{4}{5}$

Explanation:

A keyword in our question that gives us a clue that we are going to multiply to solve this problem is the word "of". $\frac{1}{5}$ of the punch is water.

We know that we have gallons of punch so we can set up our multiplication problem.

$\frac{1}{5}\times4$

4 5

$\frac{1}{5}\times4$ which means $\frac{1}{5}$ of each group of $4=\frac{4}{5}$

Report an Error

Example Question #2 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Alison made gallons of punch. $\frac{1}{3}$ of the punch was water. How much water did she use to make the punch?

Possible Answers:

$\frac{2}{3}$

$\frac{1}{3}$

$\frac{3}{3}$

Correct answer:

$\frac{2}{3}$

Explanation:

A keyword in our question that gives us a clue that we are going to multiply to solve this problem is the word "of". $\frac{1}{3}$ of the punch is water.

We know that we have gallons of punch so we can set up our multiplication problem.

$\frac{1}{3}\times2$

2 3

$\frac{1}{3}\times2$ which means $\frac{1}{3}$ of each group of $2=\frac{2}{3}$

Report an Error

Example Question #4 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Jessica made gallons of punch. $\frac{1}{4}$ of the punch was water. How much water did she use to make the punch?

Possible Answers:

$\frac{2}{4}$

$\frac{4}{4}$

$\frac{1}{4}$

Correct answer:

$\frac{2}{4}$

Explanation:

A keyword in our question that gives us a clue that we are going to multiply to solve this problem is the word "of". $\frac{1}{4}$ of the punch is water.

We know that we have gallons of punch so we can set up our multiplication problem.

$\frac{1}{4}\times2$

2 4

$\frac{1}{4}\times2$ which means $\frac{1}{4}$ of each group of $2=\frac{2}{4}$

Report an Error

View Tutors

Grace
Certified Tutor

St John's University-New York, Bachelor in Arts, Psychology. University of Bridgeport, Masters in Education, Education.

View Tutors

Marlene
Certified Tutor

Herbert Lehman, Bachelors, Recreation Education. Long Island University-Brooklyn Campus, Masters, Special Education.

View Tutors

Maddy
Certified Tutor

New York University, Bachelor in Arts, Music Theory and Composition. New York University, Masters in Education, Theater Arts.

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Phoenix, Biology Tutors in Dallas Fort Worth, Math Tutors in Philadelphia, French Tutors in Los Angeles, Computer Science Tutors in Chicago, SAT Tutors in Houston, SAT Tutors in Denver, ISEE Tutors in Houston, LSAT Tutors in Washington DC, SSAT Tutors in Denver

Popular Courses & Classes

ISEE Courses & Classes in Chicago, ISEE Courses & Classes in Miami, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in Seattle, ISEE Courses & Classes in Seattle, GRE Courses & Classes in Seattle, GRE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Chicago, Spanish Courses & Classes in Seattle, MCAT Courses & Classes in Denver

Popular Test Prep

MCAT Test Prep in Denver, ISEE Test Prep in Miami, SSAT Test Prep in Phoenix, SSAT Test Prep in Houston, GRE Test Prep in Chicago, GRE Test Prep in Dallas Fort Worth, ISEE Test Prep in Seattle, GRE Test Prep in Miami, GMAT Test Prep in Seattle, LSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : ISEE Lower Level (grades 5-6) Quantitative Reasoning

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #292 : How To Multiply Fractions

Example Question #293 : How To Multiply Fractions

Example Question #294 : How To Multiply Fractions

Example Question #2941 : Isee Lower Level (Grades 5 6) Quantitative Reasoning

Example Question #543 : Fractions

Example Question #1901 : Numbers And Operations

Example Question #1 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Example Question #2 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Example Question #2 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

Example Question #4 : Interpret The Product (A/B) × Q As A Part Of A Partition Of Q Into B Equal Parts: Ccss.Math.Content.5.Nf.B.4a

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: