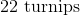Call Now to Set Up Tutoring:

(888) 888-0446

ISEE Lower Level Quantitative : How to find the solution to an equation

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

Create An Account

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : How To Find The Solution To An Equation

What is the value of the expression?

(5+3) * 2

Possible Answers:

Correct answer:

Explanation:

First you add what is inside the parentheses.

5+3=8 .

Then, we multiply,

8*2 .

This leaves us with our answer of 16.

Report an Error

Example Question #52 : How To Find The Solution To An Equation

A pencil costs $1.03 and Elena wants to purchase 386 pencils. Which expression gives the best estimate of the total cost of Alex's purchase in dollars?

Possible Answers:

1*400

1*40

130*100

130*400

10*380

Correct answer:

1*400

Explanation:

To solve, we round $1.03 to $1.00 and round 386 pencils to 400.

Then we would multiply to find the answer, so 1*400 would give us the best estimate.

Report an Error

Example Question #53 : How To Find The Solution To An Equation

Find the value of the expression.

(8-6)/2

Possible Answers:

Correct answer:

Explanation:

To solve the expression, you must first solve inside the parentheses, so

8-6=2 .

Then we divide 2 by 2 and are left with our answer, 1.

Report an Error

Example Question #54 : Equations

Caitlin received $\small x$ tickets to a concert for Friday night. She divides them equally among herself and her four friends. Which of the following expressions shows the number of tickets each person received?

Possible Answers:

$\frac{x}{5}$

x-5

$x\cdot 5$

$\frac{x}{4}$

x-4

Correct answer:

$\frac{x}{5}$

Explanation:

Including Caitlin, there are 5 total people receiving tickets.

If she is going to divide them among her friends, then we would use division,

$\frac{\text{Number of Tickets}}{\text{Number of People}}=\frac{x}{5}$

Report an Error

Example Question #55 : Equations

Solve for $\small x$ .

$\small 4x+2x-x=15$

Possible Answers:

$\small x=3$

$\small x=2$

$\small x=5$

$\small x=1$

$\small x=4$

Correct answer:

$\small x=3$

Explanation:

First we add and are left with

$\small 6x-x=15$ .

Then we subtract and are left with

$\small 5x=15$ .

Finally, in order to get the $\small x$ alone, we divide each side by 5 and are left with

$\small x=3$ .

Report an Error

Example Question #54 : How To Find The Solution To An Equation

Solve for $\small x$ .

$\small \small 1+3+(8-2)*2=x$

Possible Answers:

$\small x=16$

$\small x=13$

$\small x=19$

$\small x=12$

$\small x=20$

Correct answer:

$\small x=16$

Explanation:

Following the order of operations, we must do the work inside the parentheses first, so we are left with

$\small 1+3+6*2=x$ .

Then we must multiply and are left with

$\small 1+3+12=x$ .

Finally

$\small 4+12=x$ .

$\small x=16$ .

Report an Error

Example Question #54 : Algebraic Concepts

Five more than a number is equal to $\frac{3}{5}$ of twenty-five . What is the number?

Possible Answers:

Correct answer:

Explanation:

From the question, we know that plus a number equals $\frac{3}{5}$ of . In order to find out what $\frac{3}{5}$ of is, multiply $\frac{3}{5}$ by $\frac{25}{1}$ .

$\frac{3}{5}\times\frac{25}{1}=\frac{75}{5}$ , or .

The number we are looking for needs to be five less than , or .

You can also solve this algebraically by setting up this equation and solving:

$5+x=\frac{3}{5}\times25$

5+x=15

Subtract from both sides of the equation.

x=10

Report an Error

Example Question #58 : Equations

Solve for :

14x - 6=64

Possible Answers:

Correct answer:

Explanation:

To solve an equation, first combine like terms. Move the over to the other side of the equation by adding :

14x - 6=64

+6=+6

14x=70

Next, remove the from the variable by dividing by .

$\frac{14x}{14}=\frac{70}{14}\rightarrow x=5$

The answer is .

Report an Error

Example Question #41 : Grade 6

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

Possible Answers:

$94\ \text{turnips}$

$39\ \text{turnips}$

$22\ \text{turnips}$

$93\ \text{turnips}$

$43\ \text{turnips}$

Correct answer:

$39\ \text{turnips}$

Explanation:

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{9\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{9\ \text{corn}}{T}$

Cross multiply and solve for .

$9\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

3T=117

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{117}{3}$

Solve.

T=39

The farmer can get $39\ \text{turnips}$ .

Report an Error

Example Question #55 : How To Find The Solution To An Equation

At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade turnips for ears of corn. If a man has ears of corn, then how many turnips can he get?

Possible Answers:

$171\ \text{turnips}$

$117\ \text{turnips}$

$87\ \text{turnips}$

$127\ \text{turnips}$

$111\ \text{turnips}$

Correct answer:

$117\ \text{turnips}$

Explanation:

Ratios can be written in the following format:

$A:B\rightarrow \frac{A}{B}$

Using this format, substitute the given information to create a ratio.

$3\ \text{corn}: 13\ \text{turnips}$

Rewrite the ratio as a fraction.

$3\ \text{corn}: 13\ \text{turnips}\rightarrow \frac{3\ \text{corn}}{13\ \text{turnips}}$

We know that the farmer has ears of corn. Create a ratio with the variable that represents how many turnips he can get.

$\frac{27\ \text{corn}}{T}$

Create a proportion using the two ratios.

$\frac{3\ \text{corn}}{13\ \text{turnips}}=\frac{27\ \text{corn}}{T}$

Cross multiply and solve for .

$27\ \text{corn}\times 13\ \text{turnips}=3\ \text{corn}\times T$

Simplify.

3T=351

Divide both sides of the equation by .

$\frac{3T}{3}=\frac{351}{3}$

Solve.

T=117

The farmer can get $117\ \text{turnips}$ .

Report an Error

View Tutors

Grace
Certified Tutor

St John's University-New York, Bachelor in Arts, Psychology. University of Bridgeport, Masters in Education, Education.

View Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

View Tutors

Brianna
Certified Tutor

Florida Atlantic University, Bachelor in Arts, Psychology. Florida Memorial University, Master of Arts Teaching, Reading Teac...

All ISEE Lower Level Quantitative Resources

20 Diagnostic Tests 114 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Atlanta, Physics Tutors in Washington DC, MCAT Tutors in Chicago, SSAT Tutors in San Diego, Computer Science Tutors in Phoenix, Chemistry Tutors in Philadelphia, English Tutors in Los Angeles, MCAT Tutors in Seattle, French Tutors in San Francisco-Bay Area, GMAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

SAT Courses & Classes in Phoenix, MCAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Diego, SAT Courses & Classes in Los Angeles, LSAT Courses & Classes in Chicago, ISEE Courses & Classes in Philadelphia, Spanish Courses & Classes in Boston, ISEE Courses & Classes in Denver, ISEE Courses & Classes in Houston, GMAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

SAT Test Prep in Miami, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Philadelphia, GRE Test Prep in New York City, SAT Test Prep in Phoenix, SSAT Test Prep in Philadelphia, SAT Test Prep in New York City, GMAT Test Prep in Los Angeles, MCAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

ISEE Lower Level Quantitative : How to find the solution to an equation

Study concepts, example questions & explanations for ISEE Lower Level Quantitative

All ISEE Lower Level Quantitative Resources

Example Questions

Example Question #51 : How To Find The Solution To An Equation

Example Question #52 : How To Find The Solution To An Equation

Example Question #53 : How To Find The Solution To An Equation

Example Question #54 : Equations

Example Question #55 : Equations

Example Question #54 : How To Find The Solution To An Equation

Example Question #54 : Algebraic Concepts

Example Question #58 : Equations

Example Question #41 : Grade 6

Example Question #55 : How To Find The Solution To An Equation

All ISEE Lower Level Quantitative Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: