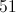First, add $\displaystyle \dpi{100} 200+50=250$.

Next, divide $\displaystyle \dpi{100} 250\div 5=50$.

So $\displaystyle \dpi{100} x=50$

When simplifying an expression, you must combine like terms. There are two types of terms in this expression: “x’s” and whole numbers.  Combine in two steps:

1) x’s:  $\displaystyle -7x+4x-x=-4x$

2) whole numbers:   $\displaystyle -11+3=-8$

The simplified expression is: $\displaystyle -4x-8$.

To solve, insert $\displaystyle -2$ for each $\displaystyle x$:

$\displaystyle -6(-2)^{2}+12(-2)+3=$

Simplify:

$\displaystyle -6(4)-24+3=$

$\displaystyle -24-24+3=-45$ 

*Common error: When solving this part of the equation  always remember the order of operations (PEMDAS) and square the number in the () BEFORE multiplying!

$\displaystyle 5(-2)^{2}-14=6$

First, you need to find what would make $\displaystyle x$ and $\displaystyle y$ true in their respective equations. $\displaystyle x$ equals 1 and $\displaystyle y$ equals 4. The next step is to add those together, which gives you 5. 

Nell's story fits best because if she bought 9 bags with 3 pieces each, that would be 27 total. This fits best with the $\displaystyle 9\times 3=27$ equation.

Find the number that makes the equation true. 2 works because when plugged in, the left side of the equation becomes 13, making the whole equation true.

From the question, we know that $\displaystyle 5$ plus a number equals $\displaystyle \frac{3}{5}$ of $\displaystyle 25$. In order to find out what $\displaystyle \frac{3}{5}$ of $\displaystyle 25$ is, multiply $\displaystyle \frac{3}{5}$ by $\displaystyle \frac{25}{1}$.  

$\displaystyle \frac{3}{5}\times\frac{25}{1}=\frac{75}{5}$, or $\displaystyle 15$.

The number we are looking for needs to be five less than $\displaystyle 15$, or $\displaystyle 10$.

You can also solve this algebraically by setting up this equation and solving:

$\displaystyle 5+x=\frac{3}{5}\times25$

$\displaystyle 5+x=15$ 

Subtract $\displaystyle 5$ from both sides of the equation.         

$\displaystyle x=10$

To solve for $\displaystyle x$, we want to isolate $\displaystyle x$, or get it by itself. 

$\displaystyle 2x-2=10$

Add $\displaystyle 2$ to both sides of the equation.

$\displaystyle 2x-2=10$

    $\displaystyle +2$        $\displaystyle +2$

$\displaystyle 2x=12$

Now we need to divide both sides by the coefficient of $\displaystyle x$, i.e. the number directly in front of the $\displaystyle x$.

$\displaystyle 2x=12$

$\displaystyle x=6$

First, subtract the three from both sides:

$\displaystyle 18-3=3x+3\left ( -3\right )$

$\displaystyle 15=3x$

Then, divide by three on both sides:

$\displaystyle \frac{15}{3}=\frac{3x}{3}$

$\displaystyle 5=x$