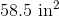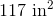All ISEE Lower Level Quantitative Resources
Example Questions
Example Question #1 : How To Find The Area Of A Triangle
What is the area of a triangle with a base of 8 and a height of 3?
The area of a triangle is 
In this case, the equation is 
Example Question #2 : How To Find The Area Of A Triangle
What is the area of a triangle that has a base of 7 and a height of 10?
To find the area of a triangle, we use 
Example Question #3 : How To Find The Area Of A Triangle
What is the area of a triangle with a base of 7cm and a height of 4cm?
Use the formula for the area of a triangle
to solve this problem. Plug in and you get 
Example Question #4 : How To Find The Area Of A Triangle
The height of a triangle is 

The formula for finding the area of a triangle is 




Example Question #5 : How To Find The Area Of A Triangle
A right triangle has a base of 4 and a height of 7.
What is the triangle's area?
An area of a triangle is
In this case
Example Question #3 : How To Find The Area Of A Triangle
If the base of a triangle is 12 cm, and the height of the triangle is 4 cm, what is the total area of the triangle?
First, you must remember the formula for the area of a triangle 
Plug in the given values: 
Multiply to get 24. Since this is area, the units must be sqaured. Therefore, your final answer is 
Example Question #45 : Triangles
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #46 : Triangles
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #3 : How To Find The Area Of A Triangle
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Example Question #51 : Triangles
What is the area of the right triangle in the following figure?

There are several different ways to solve for the area of a right triangle. In this lesson, we will transform the right triangle into a rectangle, use the the simpler formula for area of a rectangle to solve for the new figure's area, and divide this area in half in order to solve for the area of the original figure.
First, let's transform the triangle into a rectangle:

Second, let's remember that the formula for area of a rectangle is as follows:
Substitute in our side lengths.
Last, notice that our triangle is exactly half the size of the rectangle that we made. This means that in order to solve for the area of the triangle we will need to take half of the area of the rectangle, or divide it by 
Thus, the area formula for a right triangle is as follows:

Certified Tutor
All ISEE Lower Level Quantitative Resources