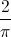We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #33 : How To Find The Volume Of A Cube

A sphere with a radius of $\frac{1}{2}$ is cut out of a cube with a side length of . What is the volume of the resulting figure?

Possible Answers:

4.12

7.48

5.02

6.67

Correct answer:

7.48

Explanation:

Since the cube is bigger, we will be subtracting the volume of the sphere from the volume of the cube.

Start by recalling how to find the volume of a sphere.

$\text{Volume of Sphere}=\frac{4}{3}\pi r^3$

Plug in the given radius to find the volume.

$\text{Volume of Sphere}=\frac{4}{3}\pi(\frac{1}{2})^3=\frac{1}{6}\pi$

Next, recall how to find the volume of a cube:

$\text{Volume of Cube}=(\text{edge})^3$

Plug in the given side length to find the volume of the cube.

$\text{Volume of Cube}=2^3=8$

Finally, subtract the volume of the sphere from the volume of the cube.

$\text{Volume of Figure}=8-\frac{1}{6}\pi=7.48$

Make sure to round to places after the decimal.

Report an Error

Example Question #34 : How To Find The Volume Of A Cube

A sphere with a radius of is cut out of a cube that has a side length of . What is the volume of the resulting figure?

Possible Answers:

65.10

74.92

98.09

101.45

Correct answer:

74.92

Explanation:

Since the cube is bigger, we will be subtracting the volume of the sphere from the volume of the cube.

Start by recalling how to find the volume of a sphere.

$\text{Volume of Sphere}=\frac{4}{3}\pi r^3$

Plug in the given radius to find the volume.

$\text{Volume of Sphere}=\frac{4}{3}\pi(4)^3=\frac{256}{3}\pi$

Next, recall how to find the volume of a cube:

$\text{Volume of Cube}=(\text{edge})^3$

Plug in the given side length to find the volume of the cube.

$\text{Volume of Cube}=7^3=343$

Finally, subtract the volume of the sphere from the volume of the cube.

$\text{Volume of Figure}=343-\frac{236}{3}\pi=74.92$

Make sure to round to places after the decimal.

Report an Error

Example Question #71 : Cubes

A sphere with a radius of $\frac{2}{3}$ is cut out of a cube that has a side length of . What is the volume of the resulting figure?

Possible Answers:

23.01

24.85

25.76

26.92

Correct answer:

25.76

Explanation:

Since the cube is bigger, we will be subtracting the volume of the sphere from the volume of the cube.

Start by recalling how to find the volume of a sphere.

$\text{Volume of Sphere}=\frac{4}{3}\pi r^3$

Plug in the given radius to find the volume.

$\text{Volume of Sphere}=\frac{4}{3}\pi(\frac{2}{3})^3=\frac{32}{81}\pi$

Next, recall how to find the volume of a cube:

$\text{Volume of Cube}=(\text{edge})^3$

Plug in the given side length to find the volume of the cube.

$\text{Volume of Cube}=3^3=27$

Finally, subtract the volume of the sphere from the volume of the cube.

$\text{Volume of Figure}=27-\frac{32}{81}\pi=25.76$

Make sure to round to places after the decimal.

Report an Error

Example Question #72 : Cubes

Pyramid

The above figure shows a triangular pyramid inscribed inside a cube. The pyramid has volume 100. Give the volume of the cube.

Possible Answers:

$666\frac{2}{3}$

400

750

800

600

Correct answer:

600

Explanation:

Let be the length of one side of the cube. Then the base of the pyramid is a right triangle with legs of length . The area of a right triangle is half the product of the lengths of the legs, so the base has area

$B = \frac{1}{2} s \cdot s = \frac{1}{2} s ^{2}$

The volume of a pyramid is one third the product of its height and the area of its base. The height of the pyramid is , so the volume is

$V_{1} = \frac{1}{3} Bh = \frac{1}{3} \cdot \frac{1}{2} s^{2} \cdot s = \frac{1}{6} s^{3}$

The volume of the cube is $V_{2} = s^{3}$ , so

$V_{1} = \frac{1}{6} V_{2}$ ,

or, equivalently,

$6 \cdot V_{1} = 6 \cdot \frac{1}{6} V_{2}$

$V_{2}= 6 \cdot V_{1}$

That is, the volume of the cube is six times that of the pyramid, and, since the pyramid has volume 100, the volume of the cube is $6 \cdot 100 =600$ .

Report an Error

Example Question #1 : Cylinders

A cylinder has a volume of 16 and a radius of 4. What is its height?

Possible Answers:

$\frac{1}{\pi}$

$\frac{2}{\pi}$

$\frac{1}{3}$

$\pi$

Correct answer:

$\frac{1}{\pi}$

Explanation:

Since the radius is 4, the area of the base is $16\pi$ . To cancel out the $\pi$ , the height must be $\frac{1}{\pi }$ .

Report an Error

Example Question #2 : Cylinders

What is the surface area of a cylinder with diameter 4 and height 6? The equation to calculate the surface area of a cylinder is:

$SA=2r^2\pi+2rh\pi$

Possible Answers:

$48\pi$

$64\pi$

$80\pi$

$32\pi$

Correct answer:

$32\pi$

Explanation:

If the diameter of the cylinder is 4, the radius is equal to 2. Therefore:

$SA=2r^2\pi+2rh\pi=2(2^2)\pi+2(2)(6)\pi=8\pi+24\pi=32\pi$

Report an Error

Example Question #71 : Solid Geometry

Find the surface area of the following right cylinder:

Cylinder33

Possible Answers:

$96\pi\ in^{2}$

$48\pi\ in^{2}$

$160\pi\ in^{2}$

$192\pi\ in^{2}$

$112\pi\ in^{2}$

Correct answer:

$112\pi\ in^{2}$

Explanation:

The answer is $112\pi\ in^{2}$ . To find the surface area we need to find the area of the top, bottom, and the round side respectively. To find the areas of the top and bottom circles, you would need to use the formula $\pi r^{2}$ .

Plug in 4 for , and you get $16\pi$ , then multiply by 2 for 2 circles to get $32\pi .$

Then to get the area of the round side, you would take the circumference times the height. Thus with the formula

$2\pi r h$

you would get $80\pi .$

To get your final answer, add $32 \pi$ and $80\pi$ to get $112\pi .$

Also you could remember the formula $SA \ cylinder = 2\left (\pi r^{2}\right )+ h\left (2\pi r \right )$

and plug in 4=r and 10=h .

Report an Error

Example Question #1 : How To Find The Surface Area Of A Cylinder

Given a cylinder with radius of 5cm and a height of 10cm, what is the surface area of the entire cylinder?

Possible Answers:

$100\pi \; cm^2$

$200\pi\; cm^2$

$50\pi\; cm^2$

$150\pi \; cm^2$

$175\pi \; cm^2$

Correct answer:

$150\pi \; cm^2$

Explanation:

The surface area of the whole cylinder = (2 * area of circle) + lateral area

Think of the lateral area as the paper label on a can; It wraps around the outside of the can while leaving the top and bottom untouched. The area of the circle, times 2, is to account for the top and the bottom of the cylinder.

Area of a circle = $\pi r^2$

So the area of the circle = $25\pi$ cm^2 , and since there are two circles we have

50cm^2

Now for the lateral area. Notice how if we have a can with a paper label, we can take the label, cut it, and unroll it from the can. In this way, our label now looks like a rectangle with a

height = height and the

width = circumference of the circle.

Circumference = $2\pi r$

So our rectangle is going to have a height of 10 and a width of 10 $\pi$ . So the lateral area =

$10\cdot 10\pi =100\pi$

So the total surface area =

$50\pi +100\pi =150\pi \ cm^{2}$

Report an Error

Example Question #4 : Cylinders

The circumference of the base of a cylinder is $6.28\:cm$ and the height of the cylinder is $12\:cm$ . What is this cylinder's surface area? Round to the tenths place.

Possible Answers:

$163.4\:cm^2$

$81.5\:cm^2$

$75.4\:cm^2$

$81.7\:cm^2$

$81.9\:cm^2$

Correct answer:

$81.7\:cm^2$

Explanation:

The formula to find the surface area of a cylinder is $A= 2 \pi rh + 2 \pi r^2$ , where is the height of the cylinder and is the radius.

In this kind of equation-based problem, it's helpful to ask "What information do I have?" and "What information is missing that I need?"

The problem provides information for the component of the equation, but not for the component. Instead, we're given information about the circumference of the circular base of the cylinder. The question that arises now is how the radius can be calculated from the circumference. The formula for circumference is: $C = \pi \cdot d$ , where is diameter. Radius can be calculated by taking half of the diameter. This means that radius and circumference are related in terms of .

Therefore, the first step for this problem is to solve for .

$C = \pi \cdot d$

$6.28 = \pi \cdot d$

$\frac{6.28}{\pi}=\frac{\pi \cdot d}{\pi}$

$d=1.99\approx2\:cm$

Because the diameter is $2\:cm$ , that means that the radius must be $1\:cm$ .

Now the surface area can be solved for after the and values are substituted into the equation.

$Area = 2 \pi (1) (12) + 2 \pi (1)^2$

$A= 2 \pi (12)+ 2 \pi (1)$

$A = 24 \pi +2\pi$

$A = 26 \pi$

$A = 81.68\:cm^2 \approx81.7\:cm^2$

Report an Error

Example Question #6 : How To Find The Surface Area Of A Cylinder

Find the surface area of the cylinder below.

Possible Answers:

1991.24

2412.74

1902.59

1988.18

Correct answer:

2412.74

Explanation:

To find the surface area of the cylinder, first find the areas of the bases:

$\text{Area of Bases}=2\pi r^2$

Next, find the lateral surface area, which is a rectangle:

$\text{Lateral Surface Area}=2\pi r h$

Add the two together to get the equation to find the surface area of a cylinder:

$\text{Surface Area of Cylinder}=2\pi r^2+2\pi r h$

Plug in the given height and radius to find the surface area.

$\text{Surface Area of Cylinder}=2\pi(12)^2+2\pi(12)(20)=768\pi=2412.74$

Make sure to round to places after the decimal point.

Report an Error

View Tutors

Sarah
Certified Tutor

View Tutors

Nafis
Certified Tutor

University of Leipzig, Germany., Bachelor of Science, Physics. University of Pittsburgh-Pittsburgh Campus, Doctor of Philosop...

View Tutors

Michelle
Certified Tutor

Virginia Union University, Bachelor in Arts, History. Howard University, Masters in Education, Auditing.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Houston, SSAT Tutors in Seattle, English Tutors in Denver, ACT Tutors in Phoenix, Chemistry Tutors in Washington DC, Algebra Tutors in Washington DC, Math Tutors in Chicago, ISEE Tutors in New York City, GRE Tutors in San Francisco-Bay Area, SSAT Tutors in San Diego

Popular Courses & Classes

MCAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Boston, ACT Courses & Classes in Seattle, Spanish Courses & Classes in New York City, GRE Courses & Classes in San Diego, MCAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Phoenix, ACT Courses & Classes in Boston, ISEE Courses & Classes in Los Angeles, LSAT Courses & Classes in Boston

Popular Test Prep

SSAT Test Prep in Miami, ACT Test Prep in Miami, ISEE Test Prep in Philadelphia, MCAT Test Prep in Miami, LSAT Test Prep in Washington DC, LSAT Test Prep in Phoenix, SSAT Test Prep in Atlanta, ISEE Test Prep in Seattle, SAT Test Prep in Boston, ISEE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #33 : How To Find The Volume Of A Cube

Example Question #34 : How To Find The Volume Of A Cube

Example Question #71 : Cubes

Example Question #72 : Cubes

Example Question #1 : Cylinders

Example Question #2 : Cylinders

Example Question #71 : Solid Geometry

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #4 : Cylinders

Example Question #6 : How To Find The Surface Area Of A Cylinder

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: