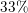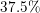Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Sectors

If you have $80\%$ of a circle, what is the angle, in degrees, that creates that region?

Possible Answers:

280

108

288

308

Correct answer:

288

Explanation:

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.

First we need to convert the percentage into a decimal.

$80\% \rightarrow \frac{80}{100}=0.8$

If you multiply 360 by 0.80, you get the degree measure that corresponds to the percentage, which is 288.

$360 \cdot 0.8= 288$

Report an Error

Example Question #12 : Circles

If you have $44\%$ of a circle, what is the angle, in degrees, that creates that region?

Possible Answers:

52.6

120

158.4

160.4

Correct answer:

158.4

Explanation:

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.

First convert the percentage into a decimal.

$44\% \rightarrow \frac{44}{100}=0.44$

If you multiply 360 by 0.44, you get the degree measure that corresponds to the percentage, which is 158.4.

$360 \cdot 0.44=158.4$

Report an Error

Example Question #13 : Circles

If you have $18\%$ of a circle, what is the angle, in degrees, that creates that region?

Possible Answers:

68.4

64.8

Correct answer:

64.8

Explanation:

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.

First convert the percentage into a decimal.

$18\% \rightarrow \frac{18}{100}=0.18$

If you multiply 360 by 0.18, you get the degree measure that corresponds to the percentage, which is 64.8.

$360 \cdot 0.18=64.8$

Report an Error

Example Question #11 : Sectors

If you have $56\%$ of a circle, what is the angle, in degrees, that creates that region?

Possible Answers:

270

200

206.1

201.6

Correct answer:

201.6

Explanation:

A full circle has 360 degrees, which means that 100% of the circle is 360 degrees.

We first need to convert the percentage into a decimal.

$56\% \rightarrow \frac{56}{100}=0.56$

If you multiply 360 by 0.56, you get the degree measure that corresponds to the percentage, which is 201.6.

$360 \cdot 0.56=201.6$

Report an Error

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

The central angle of a sector is 72^o. What percentage of the circle is comprised by the sector?

Possible Answers:

$20\%$

$10\%$

$40\%$

$80\%$

Correct answer:

$20\%$

Explanation:

The arc length of a sector, in degrees, is equal to the central angle. The total number of a degrees of a circle is 360. Therefore, we can use a proportion to calculate the percentage.

$\frac{72}{360}=\frac{x}{100}$

7200=360x

20=x

Therefore, 20% of the circle is comprised of the sector.

Report an Error

Example Question #2 : How To Find The Percentage Of A Sector From An Angle

A sector of a circle has a central angle of $\small 135^\circ$ . What percentage of the circle does the sector occupy?

Possible Answers:

$\small 24\%$

$\small 75\%$

$\small 33\%$

$\small \small 37.5\%$

$\small 15\%$

Correct answer:

$\small \small 37.5\%$

Explanation:

A whole circle is $\small 360^\circ$ . We therefore need to find the percent. We can do this by dividing.

$\small \frac{135}{360}=0.375=37.5\%$

Report an Error

Example Question #2 : How To Find The Percentage Of A Sector From An Angle

A survey was given to 250 high schoolers asking them how they got to school each day. The sector representing the students that ride the bus is 100 degrees, the sector representing the students that drive their own car is 90 degrees, and the sector representing the students that walk or ride their bike is 85 degrees. What percent of students get to school in another manner (parents drop them off, etc)?

Possible Answers:

$23.6\%$

$2.4\%$

$76.4\%$

$7.6\%$

None of the other answers.

Correct answer:

$23.6\%$

Explanation:

To find the missing percentage, first you can add the 3 sectors' angle measures together to get 275 degrees.

Then subtract that from 360 degrees because you want this missing sector, which is 85 degrees.

Then set-up a proportion:

$\frac{85}{360} = \frac{x}{100}$ and solve.

Report an Error

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

A circle graph is used to depict the results from a survey given to high school students regarding their favorite sport. The sector representing baseball measures 52 degrees. What percent of the high schoolers who took the survey prefer baseball over any other sport?

Possible Answers:

$52\%$

$14.4\%$

None of the other answers.

$15\%$

$1.44\%$

Correct answer:

$14.4\%$

Explanation:

To convert the angle of a sector in a circle to the percentage of that sector you can set-up a proportion: $\frac{52}{360} = \frac{x}{100}$ and then solve. The total number of degrees in a circle is 360, so you place 52 out of 360. The total percent being represented by a circle is 100, so you place (what you are trying to find) out of 100.

Report an Error

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

A circle graph represents the different types of pie you can find at a local bakery. The blueberry pie wedge measures 120 degrees, the apple pie wedge measures 110 degrees and the cherry pie wedge measures 130 degrees. What percent of pies in the bakery are either blueberry or cherry?

Possible Answers:

$69.4\%$

$36.1\%$

$33.3\%$

$6.9\%$

$30.6\%$

Correct answer:

$69.4\%$

Explanation:

First add together the degrees that represent blueberry and cherry pie to get 250 degrees. You want to include both sectors because the question is asking for the percent of pies that is either blueberry or cherry.

Then set up a proportion:

$\frac{250}{360} = \frac{x}{100}$ and solve for .

Report an Error

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

A circle graph represents the student population at a local high school. The sector representing boys measures 200 degrees. What percent of the high school is girls?

Possible Answers:

None of the other answers.

$4.4\%$

$44.4\%$

$5.6\%$

$55.6\%$

Correct answer:

$44.4\%$

Explanation:

First subtract 200 from 360 to get the number of degrees making up the sector representing girls.

Then set-up a proportion:

$\frac{160}{360} = \frac{x}{100}$ and solve for .

Report an Error

View Tutors

Clarissa
Certified Tutor

University of North Texas, Bachelor in Arts, International Relations.

View Tutors

Michael
Certified Tutor

Carthage College, Bachelor of Science, Finance.

View Tutors

Gabriela(Gabby)
Certified Tutor

Saint Edward's University, Bachelor of Education, Spanish Teacher Education.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Chicago, Physics Tutors in New York City, Physics Tutors in Phoenix, Physics Tutors in Chicago, LSAT Tutors in Los Angeles, GRE Tutors in Miami, GRE Tutors in San Francisco-Bay Area, Algebra Tutors in Denver, Spanish Tutors in Los Angeles, Statistics Tutors in San Francisco-Bay Area

Popular Courses & Classes

ISEE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in San Diego, LSAT Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Denver, MCAT Courses & Classes in Phoenix, SSAT Courses & Classes in Chicago, GRE Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in Atlanta, GRE Test Prep in Chicago, SAT Test Prep in Philadelphia, MCAT Test Prep in Atlanta, MCAT Test Prep in Boston, GRE Test Prep in Dallas Fort Worth, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Boston, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #11 : Sectors

Example Question #12 : Circles

Example Question #13 : Circles

Example Question #11 : Sectors

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

Example Question #2 : How To Find The Percentage Of A Sector From An Angle

Example Question #2 : How To Find The Percentage Of A Sector From An Angle

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

Example Question #1 : How To Find The Percentage Of A Sector From An Angle

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: