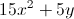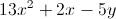Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Problem Solving

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #85 : How To Do Other Word Problems

On a particular November day, it is $115^\circ F$ and sunny in Tucson, Arizona. On the eastern side of the United States, it is $-10^\circ F$ and sleeting in New Castle, Pennsylvania. How many degrees warmer is it in Tucson than New Castle?

Possible Answers:

$123^\circ F$

$135^\circ F$

$115^\circ F$

$122^\circ F$

$125^\circ F$

Correct answer:

$125^\circ F$

Explanation:

There are several ways that we could solve this problem. First, we can say that the temperature in New Castle is $10^\circ F$ below zero and in Tucson it is $115^\circ F$ above zero; therefore we can say:

$10+115=125^\circ F$

Also, we can solve this problem by using a number line. New Castle’s temperature is units away from zero and Tucson’s is 115 units away.

Temp11

We can see that Tucson is $125^\circ F$ warmer than New Castle.

Report an Error

Example Question #561 : Problem Solving

On a particular November day, it is $120^\circ F$ and sunny in Tucson, Arizona. On the eastern side of the United States, it is $-12^\circ F$ and sleeting in New Castle, Pennsylvania. How many degrees warmer is it in Tucson than New Castle?

Possible Answers:

$123^\circ F$

$130^\circ F$

$125^\circ F$

$135^\circ F$

$132^\circ F$

Correct answer:

$132^\circ F$

Explanation:

There are several ways that we could solve this problem. First, we can say that the temperature in New Castle is $12^\circ F$ below zero and in Tucson it is $120^\circ F$ above zero; therefore we can say:

$12+120=132^\circ F$

Also, we can solve this problem by using a number line. New Castle’s temperature is units away from zero and Tucson’s is 120 units away.

Temp12

We can see that Tucson is $132^\circ F$ warmer than New Castle.

Report an Error

Example Question #2 : Use Variables To Represent Numbers And Write Expressions: Ccss.Math.Content.6.Ee.B.6

Read the following scenario:

A barista has to make sixty pounds of a special blend of coffee at Moonbucks, using Hazelnut Happiness beans and Pecan Delight beans. If there are fourteen fewer pounds of Hazelnut Happiness beans in the mixture than Pecan Delight beans, then how many pounds of each will she use?

If represents the number of pounds of Pecan Delight coffee beans in the mixture, then which of the following equations could be set up in order to find the number of pounds of each variety of bean?

Possible Answers:

x + (x - 60) = 14

x + (14-x) = 60

x + (x + 60) = 14

x + (x - 14) = 60

x + (x + 14) = 60

Correct answer:

x + (x - 14) = 60

Explanation:

Since there are fourteen fewer pounds of Hazelnut Happiness beans in the mixture than Pecan Delight beans , then the number of pounds of Hazelnut Happiness beans is fourteen subtracted from :

x -14 .

Add the number of pounds of Pecan Delight beans, , to the number of pounds of Hazelnut Happiness beans, x -14 , to get the number of pounds of the mixture, which is .

This translates to the following equation:

x + (x - 14) = 60

Report an Error

Example Question #3 : Use Variables To Represent Numbers And Write Expressions: Ccss.Math.Content.6.Ee.B.6

Read the following scenario:

A barista has to make forty pounds of a special blend of coffee at Moonbucks, using Vanilla Dream beans and Strawberry Heaven beans. If there are twelve more pounds of Vanilla Dream beans in the mixture than Strawberry Heaven beans, then how many pounds of each will she use?

If represents the number of pounds of Strawberry Heaven coffee beans in the mixture, then which of the following equations could be set up in order to find the number of pounds of each variety of bean?

Possible Answers:

x - (x + 12) = 40

x + (x - 12) = 40

x + (x + 12) = 40

x - (x + 40) = 12

x + (x + 40) = 12

Correct answer:

x + (x + 12) = 40

Explanation:

Since there are twelve more pounds of Vanilla Dream beans in the mixture than Strawberry Heaven beans, then the number of pounds of Vanilla Dream beans is twelve added to :

x + 12 .

Add the number of pounds of Strawberry Heaven beans, , to the number of pounds of Vanilla Dream beans, x + 12 , to get the number of pounds of the mixture, which is .

This translates to the following equation:

x + (x + 12) = 40

Report an Error

Example Question #562 : Problem Solving

You decide to buy a $500 table at a 20% mark down. You put a down payment of $40 then make twelve equal monthly payments. What is the amount of the payments?

Possible Answers:

$\$41.67$

$\$33.33$

$\$30$

$\$35$

$\$40$

Correct answer:

$\$30$

Explanation:

First you must find the selling price of the table since it was $500 but is now discounted 20%. Mathematically, a 20% discount is the same as the table being 80% the original price.

Also recall that a percentage can be written as a fraction or decimal.

$a\%=\frac{a}{100}=0.0a$

Set up the following formula to solve.

$\\\$500(1-0.20)= \textup{Selling Price}\\\$500(0.80)=\textup{Selling Price}\\ \\\$500\times \frac{80}{100}=\textup{Selling Price}$

Multiply across and divide to find the selling price of the table.

Multiply across results in the following.

$\$500\times 80=\$40000$

Now divide by eighty.

$\frac{\$40000}{100}=\frac{\$400\times 100}{100}=\$400$

Now subtract the down payment from the selling price to get 400-40=360 .

Finally you divide it by twelve.

$\frac{\$360}{12}=\frac{\$30\cdot 12}{12}=\$30$

Report an Error

Example Question #86 : How To Do Other Word Problems

What is the prime factorization of 48?

Possible Answers:

$\dpi{100} 2\cdot 2\cdot 12$

$\dpi{100} 4\cdot 12$

$\dpi{100} 2\cdot 24$

$\dpi{100} 2\cdot 2\cdot 2\cdot 2\cdot 3$

Correct answer:

$\dpi{100} 2\cdot 2\cdot 2\cdot 2\cdot 3$

Explanation:

We can find the prime factorization of a number by dividing 48 into smaller numbers.

$\dpi{100} 48=2\times 24$

2 is prime

$\dpi{100} 24=2\times 12$

2 is prime

$\dpi{100} 12=2\times 6$

2 is prime

$\dpi{100} 6=2\times 3$

Both 2 and 3 are prime.

So we have four 2's and one 3. Multiply these numbers to get 48.

Report an Error

Example Question #91 : How To Do Other Word Problems

How many whole numbers are between $\dpi{100} \frac{16}{5}$ and $\dpi{100} \frac{50}{7}$ ?

Possible Answers:

$\dpi{100} 3$

$\dpi{100} 6$

$\dpi{100} 2$

$\dpi{100} 4$

Correct answer:

$\dpi{100} 4$

Explanation:

Convert each fraction to a mixed number.

$\dpi{100} \frac{16}{5}=3\frac{1}{5}$

$\dpi{100} \frac{50}{7}=7\frac{1}{7}$

So how many whole numbers are between $\dpi{100} 3\frac{1}{5}$ and $\dpi{100} 7\frac{1}{7}$ ?

4, 5, 6, and 7 would fall between these two numbers. 3 would not. So there are 4 total whole numbers between them.

Report an Error

Example Question #1 : How To Simplify Expressions

You are given that A,B,C are whole numbers.

Which of the following is true of AB +C if and are both odd?

Possible Answers:

None of the other statements are true.

AB +C is always odd if is even, and always even if is odd.

AB +C is always even.

AB +C is always odd.

AB +C is always odd if is odd, and always even if is even.

Correct answer:

AB +C is always odd if is even, and always even if is odd.

Explanation:

If is odd, then is odd, since the product of two odd whole numbers must be odd. When the odd number is added, the result, AB +C , is even, since the sum of two odd numbers must be even.

If is even, then is even, since the product of an odd number and an even number must be even. When the odd number is added, the result, AB +C , is odd, since the sum of an odd number and an even number must be odd.

Report an Error

Example Question #2 : How To Simplify Expressions

Simplify the expression:

3x^2+9x+10x^2+5y+(-11x)

Possible Answers:

11x^2+5y

13x^2-2x+5y

13x^2+2x-5y

15x^2+5y

Correct answer:

13x^2-2x+5y

Explanation:

Combine all the like terms.

The x^2 terms can be combined together, which gives you 13x^2 .

When you combine the terms together, you get -2x .

There is only one term so it doesn't get combined with anything. Put them all together and you get

13x^2-2x+5y .

Report an Error

Example Question #3 : How To Simplify Expressions

Simplify the following expression:

$\dpi{100} \small 2(4x-3x)-6t+5x$

Possible Answers:

$\dpi{100} \small 14x - 11xt$

$\dpi{100} \small 6x+11x$

$\dpi{100} \small 6t-7x$

$\dpi{100} \small 1x-6t+5$

$\dpi{100} \small 7x-6t$

Correct answer:

$\dpi{100} \small 7x-6t$

Explanation:

$\dpi{100} \small 2(4x-3x)-6t+5x$

First distribute the 2: $\dpi{100} \small 8x-6x-6t+5x$

Combine the like terms: $\dpi{100} \small 7x-6t$

Report an Error

View Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Sanford
Certified Tutor

Westminster College, Bachelor of Science, Social Studies Teacher Education.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in New York City, LSAT Tutors in Seattle, Reading Tutors in Houston, Calculus Tutors in Boston, SSAT Tutors in Boston, Computer Science Tutors in Chicago, English Tutors in Dallas Fort Worth, ACT Tutors in Miami, French Tutors in Houston, French Tutors in San Diego

Popular Courses & Classes

LSAT Courses & Classes in Atlanta, GRE Courses & Classes in New York City, GRE Courses & Classes in Atlanta, MCAT Courses & Classes in Chicago, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in San Diego, ISEE Courses & Classes in New York City, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Phoenix, GRE Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in Los Angeles, ACT Test Prep in Miami, LSAT Test Prep in Miami, ISEE Test Prep in Seattle, MCAT Test Prep in Seattle, SSAT Test Prep in Atlanta, ISEE Test Prep in Chicago, GRE Test Prep in Seattle, MCAT Test Prep in Miami, ACT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Problem Solving

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #85 : How To Do Other Word Problems

Example Question #561 : Problem Solving

Example Question #2 : Use Variables To Represent Numbers And Write Expressions: Ccss.Math.Content.6.Ee.B.6

Example Question #3 : Use Variables To Represent Numbers And Write Expressions: Ccss.Math.Content.6.Ee.B.6

Example Question #562 : Problem Solving

Example Question #86 : How To Do Other Word Problems

Example Question #91 : How To Do Other Word Problems

Example Question #1 : How To Simplify Expressions

Example Question #2 : How To Simplify Expressions

Example Question #3 : How To Simplify Expressions

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: